Find 1/2 Of 5 Less Than 10
listenit
May 25, 2025 · 5 min read
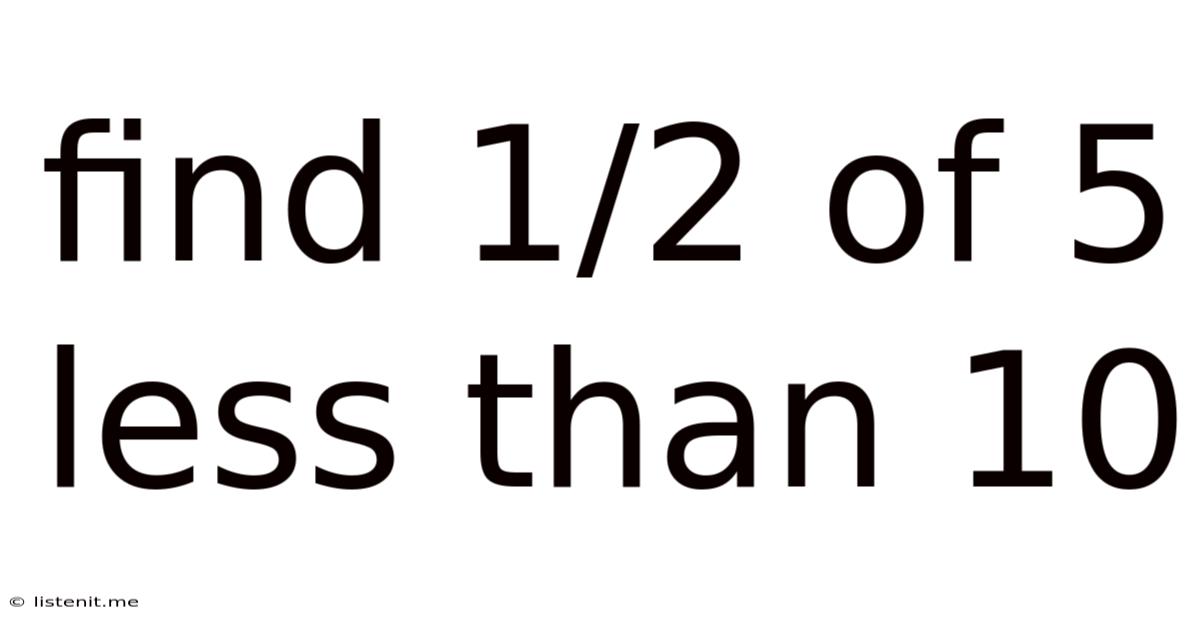
Table of Contents
Find 1/2 of 5 Less Than 10: A Deep Dive into Mathematical Problem Solving
This seemingly simple math problem, "Find 1/2 of 5 less than 10," presents a fantastic opportunity to explore fundamental mathematical concepts and problem-solving strategies. While the solution itself is straightforward, the process of arriving at the answer offers valuable insights into order of operations, fraction manipulation, and the importance of clear, step-by-step reasoning. This article will dissect this problem, examining it from various perspectives and extending the learning to more complex scenarios.
Understanding the Problem: Deconstructing the Phrase
The core challenge lies in accurately interpreting the phrasing of the problem. The key is understanding the implied order of operations. "1/2 of 5 less than 10" is not simply "1/2 * 5 - 10". Instead, we must first determine what "5 less than 10" represents.
Order of Operations: PEMDAS/BODMAS
The acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) helps us remember the standard order of operations. In this case, "5 less than 10" translates to a subtraction operation that must be performed before any multiplication involving the fraction.
Therefore, the problem correctly translates to:
1/2 * (10 - 5)
Step-by-Step Solution: A Clear Path to the Answer
Now that we've correctly interpreted the problem, let's solve it step-by-step:
-
Parentheses/Brackets First: We begin by solving the expression within the parentheses: 10 - 5 = 5. This simplifies the problem to:
1/2 * 5
-
Multiplication: Next, we perform the multiplication: 1/2 * 5 = 5/2 or 2.5.
Therefore, the answer to "Find 1/2 of 5 less than 10" is 2.5.
Expanding the Concept: Beyond the Basic Problem
While the solution is simple, let's explore how this problem can be extended to develop a deeper understanding of related mathematical concepts.
Working with Different Fractions: Exploring Variations
Let's change the fraction. What if the problem was "Find 2/3 of 5 less than 10"? The process remains the same:
-
Parentheses/Brackets First: 10 - 5 = 5
-
Multiplication: 2/3 * 5 = 10/3 or approximately 3.33
This variation highlights the versatility of the problem-solving approach and the importance of understanding fraction multiplication.
Incorporating Variables: Introduction to Algebra
We can introduce algebraic elements to enhance the complexity. Let's consider a problem like: "Find x/y of 'a' less than 'b'".
This requires substituting variables and following the same order of operations:
-
Parentheses/Brackets First: b - a
-
Multiplication: (x/y) * (b - a)
This demonstrates how the core principles remain applicable even when dealing with abstract variables. Understanding this foundational step is crucial for more advanced algebraic manipulations.
Real-World Applications: Practical Examples
This type of problem isn't just an abstract exercise; it finds real-world applications in various scenarios. Consider these examples:
-
Sharing Resources: Imagine you have 10 apples and want to give half of what remains after giving 5 apples away. This perfectly mirrors the structure of the original problem.
-
Discounts and Sales: A store offers a 50% discount on an item after a $5 reduction. This translates directly into the mathematical structure we've analyzed.
-
Recipe Adjustments: If a recipe calls for 10 cups of flour but you want to use half of what remains after removing 5 cups, the problem-solving strategy applies again.
These real-world connections underscore the practicality and relevance of seemingly simple mathematical problems.
Problem-Solving Strategies: Developing Critical Thinking
The problem "Find 1/2 of 5 less than 10" is not just about finding the numerical answer; it's about mastering the underlying problem-solving process. Here are some key strategies that can be applied:
-
Breaking Down the Problem: Analyzing the problem phrase by phrase, identifying keywords, and translating words into mathematical symbols is crucial.
-
Visual Representation: For some, visualizing the problem using diagrams or models might aid in understanding the sequence of operations.
-
Checking your Work: Always verify your answer. You can do this by substituting your answer back into the original problem to see if it makes sense.
-
Practice and Repetition: Consistent practice with similar problems strengthens your understanding of order of operations and problem-solving techniques.
Expanding Mathematical Skills: Moving Towards Advanced Concepts
This simple problem forms a strong foundation for more advanced mathematical concepts. The understanding of order of operations is fundamental to algebra, calculus, and various other branches of mathematics. The ability to manipulate fractions is crucial for working with ratios, proportions, and percentages.
The problem-solving skills developed by tackling this seemingly simple challenge are transferable to more intricate mathematical and real-world problems. It teaches the importance of precision, step-by-step reasoning, and the ability to translate words into mathematical expressions—all essential skills for success in mathematics and beyond.
Conclusion: The Power of Simple Problems
The problem "Find 1/2 of 5 less than 10" might appear trivial, but it serves as a powerful tool for illustrating fundamental mathematical principles and problem-solving strategies. By understanding the order of operations, mastering fraction manipulation, and developing strong problem-solving techniques, you build a solid foundation for tackling more complex mathematical challenges. The ability to break down a problem into smaller, manageable steps and apply these skills to real-world situations is a valuable asset that extends far beyond the realm of mathematics. Remember, mastering the basics is the key to unlocking more advanced concepts and achieving greater success in your mathematical journey.
Latest Posts
Latest Posts
-
6 Months From July 29 2024
May 25, 2025
-
How Many Days Since Oct 11
May 25, 2025
-
What Is 1 30 As A Percent
May 25, 2025
-
What Is The Gcf Of 77 And 56
May 25, 2025
-
What Is The Percent Of 6 10
May 25, 2025
Related Post
Thank you for visiting our website which covers about Find 1/2 Of 5 Less Than 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.