Divide The Difference Between 1200 And 700 By 5
listenit
May 24, 2025 · 5 min read
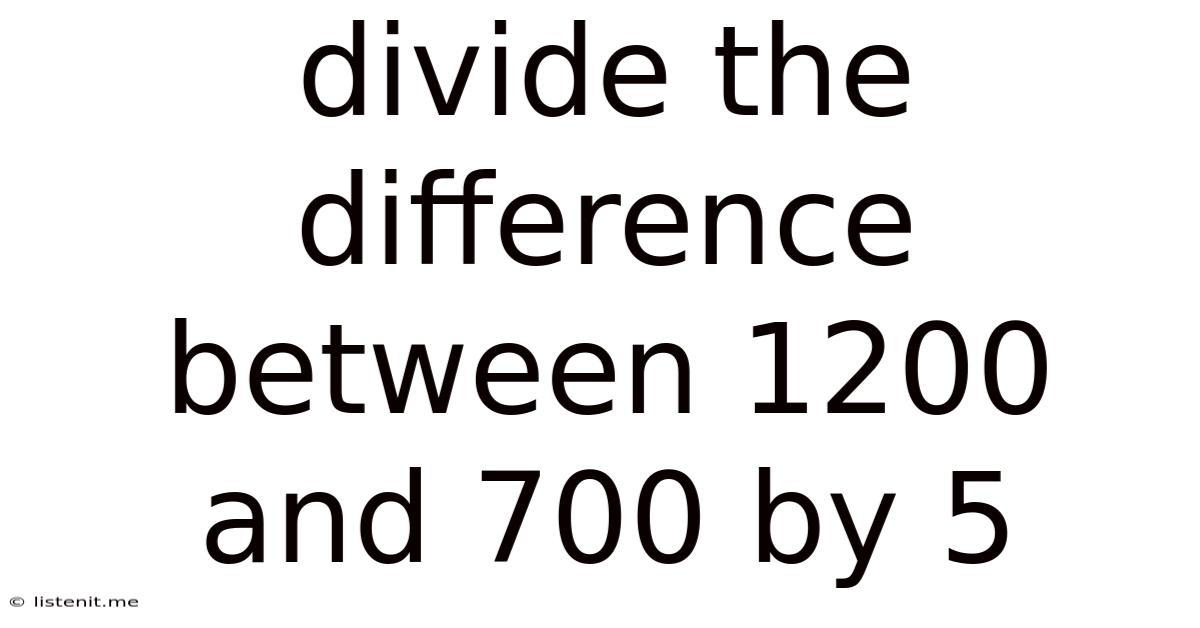
Table of Contents
Dividing the Difference: A Deep Dive into Mathematical Concepts and Practical Applications
This seemingly simple mathematical problem – dividing the difference between 1200 and 700 by 5 – opens a door to a wide range of mathematical concepts and practical applications. While the solution itself is straightforward, exploring the underlying principles and expanding upon the problem provides a rich learning experience. This article delves into the step-by-step solution, explores related mathematical concepts, and examines real-world scenarios where this type of calculation proves invaluable.
Step-by-Step Solution
The problem asks us to perform a series of operations: finding the difference between two numbers, and then dividing that difference by another number. Let's break it down:
-
Find the Difference: The first step is to determine the difference between 1200 and 700. This is a simple subtraction problem: 1200 - 700 = 500.
-
Divide the Difference: The next step is to divide the difference (500) by 5. This is another simple division problem: 500 / 5 = 100.
Therefore, the answer to the problem "divide the difference between 1200 and 700 by 5" is 100.
Expanding the Mathematical Concepts
This seemingly simple calculation touches upon several fundamental mathematical concepts:
-
Subtraction: The core operation of finding the difference between two numbers. Understanding subtraction is crucial for various mathematical applications, from simple arithmetic to advanced calculus.
-
Division: The process of dividing a number into equal parts. This operation is essential for numerous applications, including sharing resources, calculating averages, and understanding ratios.
-
Order of Operations (PEMDAS/BODMAS): While this specific problem doesn't involve complex expressions, understanding the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) is crucial for solving more complicated mathematical problems. In this case, subtraction is performed before division.
-
Integers: The numbers involved (1200, 700, 5, and 100) are all integers – whole numbers without fractions or decimals. Working with integers is fundamental to arithmetic and forms the basis for understanding more advanced number systems.
-
Real Numbers: Expanding further, these numbers are also real numbers, a set that includes all rational (integers and fractions) and irrational numbers (numbers that cannot be expressed as a simple fraction, like pi).
Real-World Applications: Where This Calculation Matters
The seemingly simple calculation of dividing the difference between two numbers has a surprisingly broad range of applications in real life:
-
Budgeting and Finance: Imagine you have a budget of $1200 and you've already spent $700. Dividing the remaining amount ($500) by 5 could help you determine how much you can spend each day for the next 5 days.
-
Resource Allocation: Suppose a company has 1200 units of a resource and has already used 700. Dividing the remaining 500 units by 5 could represent the daily allocation for the next five days of operation.
-
Average Calculations: Consider a scenario where the temperature over five days reached highs of 1200, 1100, 1000, 900, and 700 degrees in some arbitrary unit. Finding the average temperature would require calculating the difference between the highest and lowest temperatures (1200 - 700 = 500), but further steps would be required to arrive at the average.
-
Data Analysis: In data analysis, subtracting two values and dividing the result represents a simplified form of calculating a rate of change or trend.
-
Profit and Loss Calculations: If a business had a revenue of 1200 units and expenses of 700 units, dividing the profit (500 units) by 5 might show the average daily profit.
-
Construction and Engineering: Many construction and engineering tasks involve calculating distances, volumes, and other quantities. Subtracting one measurement from another and then dividing by a constant factor is often essential for determining ratios, proportions, and averages.
Expanding on the Problem: Introducing Variables
Let's generalize the problem by introducing variables:
Let 'a' represent the larger number (1200), 'b' represent the smaller number (700), and 'c' represent the divisor (5). The problem can then be expressed as: (a - b) / c.
This representation allows us to solve similar problems with different numbers without repeating the entire process. For example:
- If a = 1500, b = 800, and c = 10, then (1500 - 800) / 10 = 70.
- If a = 2000, b = 1000, and c = 2, then (2000 - 1000) / 2 = 500.
This generalized form demonstrates the power of algebra in simplifying and solving a wide range of problems.
Further Exploration: Connecting to Other Mathematical Fields
This simple problem can serve as a stepping stone to more advanced mathematical concepts:
-
Calculus: The concept of difference quotients in calculus builds upon the idea of finding the difference between two values and dividing by the difference in their inputs. This forms the foundation for understanding derivatives and rates of change.
-
Statistics: Finding differences and averages are fundamental operations in statistical analysis. Calculating the range of a dataset (the difference between the highest and lowest values) is a direct application of subtraction.
-
Linear Algebra: Vectors and matrices often involve operations similar to subtraction and division. Understanding these basic arithmetic operations forms the base for linear algebra concepts.
Conclusion: The Power of Simplicity
The seemingly simple problem of dividing the difference between 1200 and 700 by 5 illustrates the importance of fundamental mathematical concepts. While the answer itself is straightforward (100), the underlying principles and the broad range of applications demonstrate the power and practicality of even the most basic arithmetic operations. From budgeting and finance to data analysis and advanced mathematics, this simple calculation serves as a reminder of the ubiquitous nature of mathematical principles in our daily lives. Understanding these principles and their applications equips us to solve more complex problems and tackle real-world challenges more effectively. The ability to generalize this type of problem using variables further highlights the power of mathematical thinking and its application in various fields.
Latest Posts
Latest Posts
-
16 2 Is What Percent Of 45
May 24, 2025
-
Mean And Standard Deviation Of Sampling Distribution Calculator
May 24, 2025
-
What Is The Greatest Common Factor Of 8 And 32
May 24, 2025
-
What Time Will It Be In Nine Hours
May 24, 2025
-
10 Miles Per Second To Mph
May 24, 2025
Related Post
Thank you for visiting our website which covers about Divide The Difference Between 1200 And 700 By 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.