Divide 66 By Half And Add 33
listenit
May 24, 2025 · 4 min read
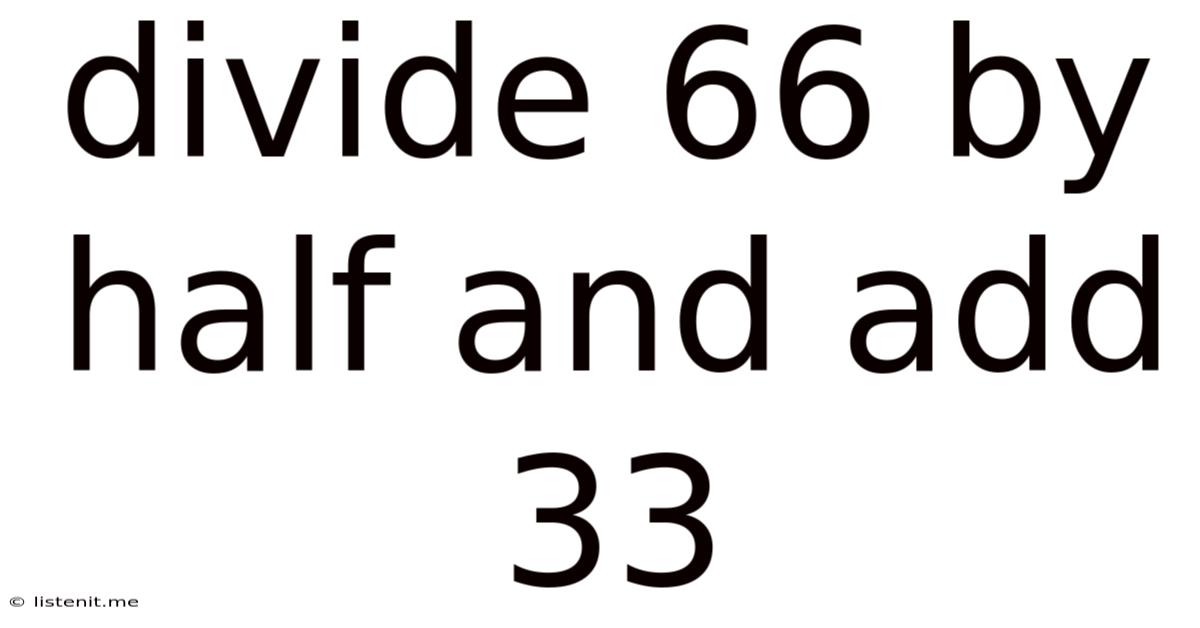
Table of Contents
Divide 66 by Half and Add 33: A Deep Dive into Mathematical Concepts and Problem-Solving
This seemingly simple math problem, "Divide 66 by half and add 33," is a fantastic springboard for exploring several key mathematical concepts and problem-solving strategies. It's deceptively tricky, highlighting the importance of precise language and careful interpretation in mathematics. Let's unpack it step-by-step.
Understanding the Problem: The Importance of Precision
The key to solving this problem lies in understanding the phrase "divide 66 by half." Many people mistakenly interpret this as dividing 66 by 0.5 (or 1/2). While this is a valid mathematical operation, it’s not the intended interpretation here. The phrase "divide by half" implies dividing by one half, which means multiplying by the reciprocal of one-half, which is 2.
Therefore, the problem is actually:
(66 x 2) + 33 = ?
Step-by-Step Solution
-
Division by Half: The first step is to divide 66 by half, which is equivalent to multiplying 66 by 2.
66 x 2 = 132
-
Addition: The second step involves adding 33 to the result obtained in step 1.
132 + 33 = 165
Therefore, the solution to the problem "Divide 66 by half and add 33" is 165.
Beyond the Numbers: Exploring Related Mathematical Concepts
This simple problem opens doors to exploring several important mathematical ideas:
1. Order of Operations (PEMDAS/BODMAS)
The order of operations, often remembered using the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), dictates the sequence in which calculations should be performed. In this problem, the multiplication (dividing by half) takes precedence over the addition. Understanding the order of operations is crucial for accurately solving complex mathematical expressions.
2. Fractions and Reciprocals
The problem highlights the relationship between fractions and their reciprocals. Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of 1/2 is 2/1 or simply 2. This concept is fundamental in algebra and many other areas of mathematics.
3. Ambiguity in Language and the Importance of Clear Communication
This particular problem underscores the importance of precise language in mathematics. The phrasing "divide 66 by half" could be misinterpreted. Precise wording is crucial to avoid ambiguity and ensure clear communication in all mathematical problems, particularly in collaborative efforts or when presenting solutions to others.
4. Problem-Solving Strategies
Solving this problem involves a simple yet powerful problem-solving strategy: breaking down a complex problem into smaller, manageable steps. This approach is applicable to a wide range of mathematical and real-world problems.
Expanding the Scope: Similar Problems and Applications
Let’s look at similar problems and how the concepts discussed above apply:
Example 1: Divide 100 by one-third and subtract 20.
This problem involves dividing by a fraction (1/3). The correct approach is to multiply by the reciprocal (3).
- Divide 100 by one-third: 100 x 3 = 300
- Subtract 20: 300 - 20 = 280
The answer is 280.
Example 2: Divide 24 by half, add 12, and multiply by 5.
- Divide 24 by half: 24 x 2 = 48
- Add 12: 48 + 12 = 60
- Multiply by 5: 60 x 5 = 300
The answer is 300.
These examples showcase the consistent application of the principles explained earlier: understanding the meaning of "divide by half," adhering to the order of operations, and utilizing the concept of reciprocals when working with fractions.
Real-world Applications
Although seemingly simple, the concepts within this math problem have broad real-world applications:
-
Cooking and Baking: Scaling recipes up or down often involves multiplying or dividing ingredient quantities by fractions. Understanding fraction manipulation is crucial here.
-
Construction and Engineering: Precise measurements and calculations are essential, and dividing quantities by fractions is frequent.
-
Finance: Calculating interest, discounts, or proportions of investments involves similar mathematical operations.
-
Data Analysis: Data analysis and manipulation often require dividing and multiplying quantities, including dealing with fractions and proportions.
-
Programming: Programmers frequently encounter similar operations when processing data or performing calculations.
Conclusion: More Than Just a Math Problem
The seemingly trivial problem, "Divide 66 by half and add 33," reveals deeper insights into fundamental mathematical concepts and problem-solving approaches. It emphasizes the importance of precise language, understanding the order of operations, and recognizing the relationship between fractions and reciprocals. These concepts, far from being limited to theoretical mathematics, have extensive applications in diverse real-world contexts. By carefully dissecting this problem, we gain a valuable appreciation for the power and precision required in mathematical reasoning. Its simplicity belies its significance as a tool for understanding and sharpening our mathematical skills. The answer, 165, is more than just a numerical result; it represents a deeper understanding of the underlying mathematical principles at play. This problem serves as a potent reminder that even seemingly simple problems can reveal rich mathematical insights and practical applications.
Latest Posts
Latest Posts
-
What Is The Least Common Multiple Of 3 And 16
May 24, 2025
-
What Is 16 12 In Simplest Form
May 24, 2025
-
What Is 1 3 4 Divided By 2 As A Fraction
May 24, 2025
-
The Date 21 Days From Today
May 24, 2025
-
How Much Is 30 Of 300
May 24, 2025
Related Post
Thank you for visiting our website which covers about Divide 66 By Half And Add 33 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.