Common Factors Of 60 And 70
listenit
May 25, 2025 · 5 min read
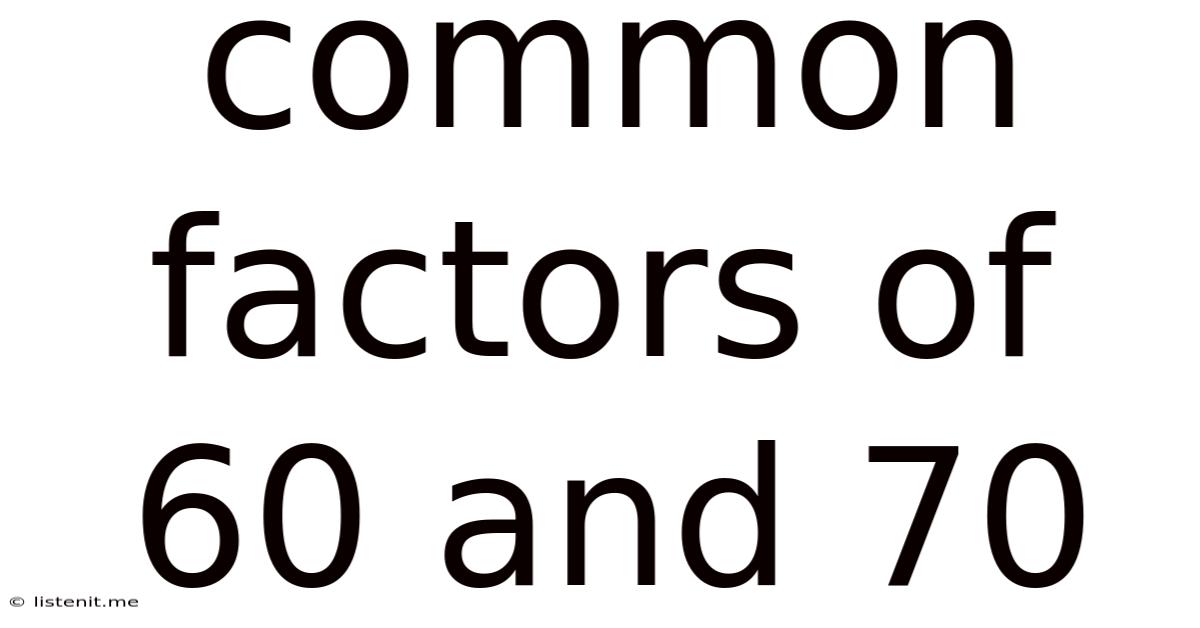
Table of Contents
Unveiling the Common Factors of 60 and 70: A Deep Dive into Number Theory
Finding the common factors of two numbers might seem like a simple task, particularly with relatively small numbers like 60 and 70. However, understanding the process reveals fundamental concepts in number theory, offering a gateway to more complex mathematical explorations. This article delves into the common factors of 60 and 70, explaining the methods, highlighting the underlying principles, and extending the concepts to broader applications.
Understanding Factors and Common Factors
Before embarking on our journey to find the common factors of 60 and 70, let's clarify some key terms:
-
Factor: A factor of a number is a whole number that divides the number without leaving a remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12.
-
Common Factor: A common factor of two or more numbers is a factor that is shared by all of them. For example, the common factors of 12 and 18 are 1, 2, 3, and 6.
-
Greatest Common Factor (GCF): Also known as the highest common factor (HCF), this is the largest common factor among two or more numbers. The GCF of 12 and 18 is 6.
Finding the Factors of 60 and 70
To discover the common factors, we first need to identify all the factors of 60 and 70 individually. There are several ways to do this:
Method 1: Systematic Listing
We systematically list all the numbers that divide 60 and 70 without leaving a remainder:
Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Factors of 70: 1, 2, 5, 7, 10, 14, 35, 70
Method 2: Prime Factorization
Prime factorization breaks down a number into its prime factors – numbers divisible only by 1 and themselves. This method is particularly useful for larger numbers.
Prime factorization of 60: 2 x 2 x 3 x 5 = 2² x 3 x 5
Prime factorization of 70: 2 x 5 x 7
Identifying Common Factors
By comparing the lists of factors for 60 and 70, we can easily pinpoint the common factors:
Common factors of 60 and 70: 1, 2, 5, and 10
Determining the Greatest Common Factor (GCF)
From the list of common factors, we can readily identify the greatest common factor (GCF) of 60 and 70, which is 10.
Alternative Method: Using Prime Factorization to Find the GCF
The prime factorization method offers an elegant way to find the GCF. By examining the prime factorizations of 60 (2² x 3 x 5) and 70 (2 x 5 x 7), we identify the common prime factors: 2 and 5.
To calculate the GCF, we multiply the common prime factors raised to their lowest power:
2¹ x 5¹ = 10
This confirms that the GCF of 60 and 70 is indeed 10.
Applications of Finding Common Factors and GCF
Understanding common factors and the GCF has far-reaching applications in various mathematical and real-world contexts:
1. Simplifying Fractions:
The GCF is crucial in simplifying fractions to their lowest terms. For example, the fraction 60/70 can be simplified by dividing both the numerator and denominator by their GCF (10), resulting in the equivalent fraction 6/7.
2. Solving Problems Involving Ratios and Proportions:
Many problems involving ratios and proportions require finding the GCF to simplify the ratio to its simplest form. This simplifies calculations and makes comparisons easier.
3. Geometry and Measurement:
The GCF plays a role in geometry when dealing with problems involving area, perimeter, and volume. For instance, finding the largest square tile that can perfectly cover a rectangular floor with dimensions 60 cm and 70 cm involves finding the GCF of 60 and 70, which is 10 cm.
4. Number Theory and Cryptography:
The concepts of factors, common factors, and the GCF are fundamental in number theory, forming the basis for more advanced concepts like modular arithmetic and cryptography. These concepts have applications in securing online transactions and data protection.
5. Everyday Applications:
Even in everyday life, the concept of common factors can be implicitly used. Imagine you have 60 apples and 70 oranges, and you want to divide them into equal bags without any leftovers. You would need to find the GCF (10) to determine the maximum number of bags you can make.
Expanding the Concept: Least Common Multiple (LCM)
While we have focused on common factors and the GCF, it's important to also consider the least common multiple (LCM). The LCM is the smallest number that is a multiple of two or more given numbers.
Finding the LCM of 60 and 70 can be done through several methods, including listing multiples or using prime factorization. The prime factorization method involves finding the prime factors of each number and multiplying the highest powers of all prime factors present in either number.
Prime factorization of 60: 2² x 3 x 5
Prime factorization of 70: 2 x 5 x 7
LCM of 60 and 70: 2² x 3 x 5 x 7 = 420
The LCM is useful in various applications, including:
-
Adding and subtracting fractions with different denominators: The LCM of the denominators is used to find a common denominator.
-
Scheduling and cyclical events: Finding the LCM can help determine when two cyclical events will occur simultaneously. For example, if event A happens every 60 days and event B every 70 days, they will both occur together again after 420 days.
Conclusion: The Significance of Understanding Common Factors
Understanding common factors, the GCF, and the LCM is essential for a deeper grasp of number theory and its applications. While finding the common factors of 60 and 70 may appear simple at first glance, the process underscores fundamental concepts that extend to more complex mathematical problems and real-world scenarios. Mastering these concepts provides a strong foundation for tackling more advanced mathematical challenges and opens doors to further exploration in areas like algebra, geometry, and cryptography. The seemingly straightforward exercise of identifying the common factors of 60 and 70 serves as a gateway to a fascinating world of mathematical exploration and practical applications.
Latest Posts
Latest Posts
-
How Many Square Feet Is 6x8
May 26, 2025
-
What Is 3 3 3 3 3
May 26, 2025
-
How Many Calories Are In Weight Watchers Points
May 26, 2025
-
30 Days After October 11 2024
May 26, 2025
-
14 Divided By 3 With Remainder
May 26, 2025
Related Post
Thank you for visiting our website which covers about Common Factors Of 60 And 70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.