14 Divided By 3 With Remainder
listenit
May 26, 2025 · 5 min read
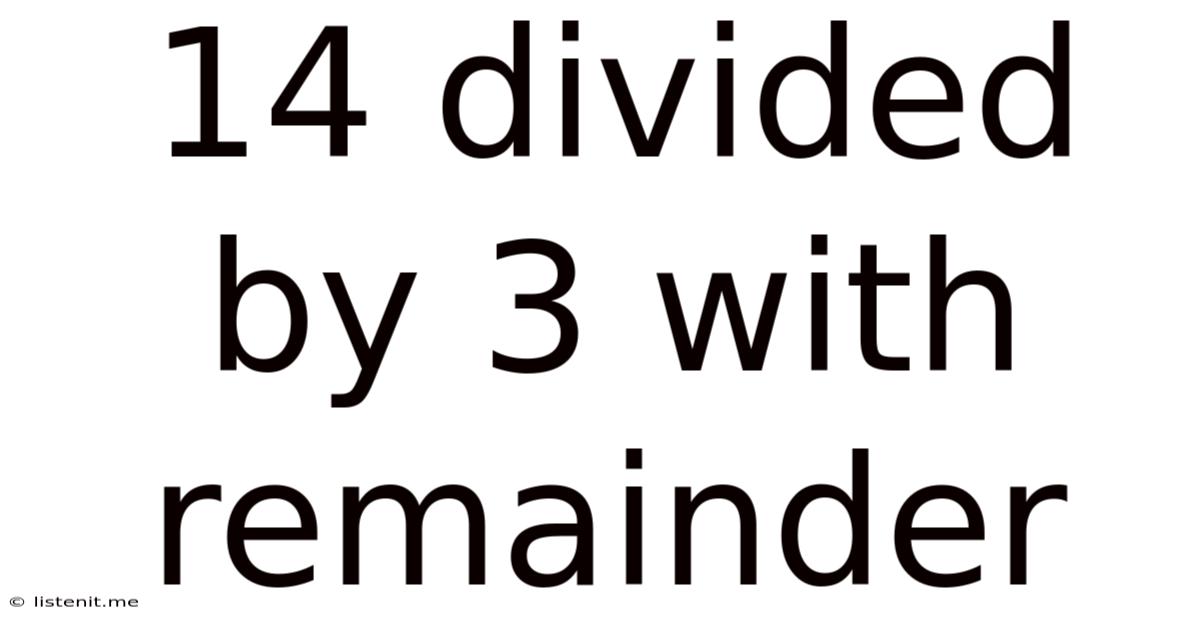
Table of Contents
14 Divided by 3 with Remainder: A Deep Dive into Division with Remainders
Division, a fundamental arithmetic operation, forms the bedrock of many mathematical concepts. Understanding division, particularly division with remainders, is crucial for various applications, from everyday calculations to advanced mathematical problem-solving. This article will delve deep into the concept of 14 divided by 3 with a remainder, exploring the mechanics, applications, and broader implications of this seemingly simple division problem.
Understanding Division and Remainders
Division involves splitting a whole number (the dividend) into equal parts, determined by another whole number (the divisor). The result is the quotient, representing the number of equal parts obtained. However, not all divisions result in perfectly equal parts. When the dividend isn't perfectly divisible by the divisor, a remainder is left over. This remainder represents the portion of the dividend that wasn't fully divided.
In the context of 14 divided by 3, we're asking: "How many times does 3 go into 14, and what's left over?"
The Calculation: 14 ÷ 3
Let's perform the division:
- Find the quotient: We determine how many times 3 fits completely into 14. 3 goes into 14 four times (3 x 4 = 12). This is our quotient.
- Calculate the remainder: We subtract the product (12) from the dividend (14). 14 - 12 = 2. This is our remainder.
Therefore, 14 divided by 3 is 4 with a remainder of 2. This can be expressed mathematically as:
14 ÷ 3 = 4 R 2
or
14 = 3 x 4 + 2
This second representation highlights the fundamental relationship between the dividend, divisor, quotient, and remainder.
Real-World Applications of Remainders
While seemingly simple, understanding remainders has practical applications in diverse fields:
1. Everyday Life: Sharing and Distribution
Imagine you have 14 cookies to share equally among 3 friends. Dividing 14 by 3 (14 ÷ 3 = 4 R 2) reveals you can give each friend 4 cookies, and you'll have 2 cookies left over.
2. Programming and Computer Science: Modular Arithmetic
Remainders are fundamental to modular arithmetic, a branch of number theory with applications in cryptography, computer science, and digital signal processing. The modulo operator (%) calculates the remainder after division. For example, in many programming languages, 14 % 3 would return 2. This is crucial for tasks like creating cyclical patterns, managing data structures, and ensuring data integrity.
3. Engineering and Design: Pattern Repetition and Measurement
Remainders are important in engineering designs that involve repetitive patterns or precise measurements. If you're designing a tiled floor with tiles 3 units wide, and you have a space 14 units wide, you'll need 4 full tiles (4 x 3 = 12 units) with 2 units remaining, requiring a custom-sized tile or adjustment to the design.
4. Time and Calendars: Date Calculations
Remainders are essential in calculating dates and days of the week. For example, determining the day of the week for a future date often involves considering remainders when dividing by 7 (the number of days in a week).
5. Mathematics: Number Theory and Algebra
Remainders play a vital role in more advanced mathematical concepts like modular arithmetic, congruences, and group theory. They are used to solve complex equations and understand the properties of numbers.
Expanding the Concept: Exploring Larger Numbers
The concept of division with remainders scales to larger numbers. Let's explore a slightly more complex example:
Example: Divide 143 by 12.
- Divide: 12 goes into 14 once (12 x 1 = 12).
- Subtract: 14 - 12 = 2. Bring down the next digit (3), making it 23.
- Divide: 12 goes into 23 once (12 x 1 = 12).
- Subtract: 23 - 12 = 11. This is our remainder.
Therefore, 143 ÷ 12 = 11 R 11. This can also be written as 143 = 12 x 11 + 11.
Different Notations for Remainders
The remainder is usually denoted by the letter "R". However, depending on the context, different notations might be used:
- R: This is the most common notation (e.g., 14 ÷ 3 = 4 R 2).
- Modulus Operator (%): In programming and some mathematical contexts, the modulo operator (%) is used to represent the remainder (e.g., 14 % 3 = 2).
- Fractional Representation: The remainder can be incorporated into a fractional part of the quotient (e.g., 14 ÷ 3 = 4 ⅔). This represents the remainder as a fraction of the divisor.
The Significance of the Remainder in Different Contexts
The interpretation and significance of the remainder depend heavily on the context of the problem.
- Equal Sharing: In scenarios involving equal sharing, the remainder signifies the leftover quantity that cannot be distributed evenly.
- Cyclic Processes: In cyclical processes or repetitive patterns, the remainder indicates the position or phase within the cycle.
- Modular Arithmetic: In modular arithmetic, the remainder is the core result, representing the equivalence class modulo the divisor.
Advanced Applications and Connections
The seemingly simple concept of division with remainders has surprisingly far-reaching implications in diverse areas:
- Cryptography: Modular arithmetic, which heavily relies on remainders, forms the foundation of many modern encryption algorithms.
- Computer Graphics: Remainders are utilized in generating repetitive textures and patterns in computer graphics and image processing.
- Data Structures: Hashing algorithms, used to organize and retrieve data efficiently, often employ the modulo operator to distribute data across different memory locations.
- Game Development: Remainders are used to control game mechanics, create animations, and manage random events.
Conclusion: The Power of Remainders
The humble remainder, often overlooked in basic arithmetic, plays a surprisingly significant role in a wide range of applications. From everyday tasks to complex computational algorithms, understanding division with remainders is essential for anyone seeking a deeper grasp of mathematics and its applications in the real world. The seemingly simple equation, 14 divided by 3 with a remainder of 2, unlocks a world of mathematical possibilities and practical uses, demonstrating the power of seemingly simple concepts in solving complex problems. The importance of understanding remainders extends beyond basic arithmetic, reaching into higher-level mathematics, computer science, and various other fields, solidifying its position as a crucial mathematical concept.
Latest Posts
Latest Posts
-
How Many Btus To Heat 600 Square Feet
May 26, 2025
-
12 4 5 X 15 4
May 26, 2025
-
What Is 17 Out Of 22 As A Percentage
May 26, 2025
-
X 1 2 X 1 2
May 26, 2025
-
What Are The Common Factors Of 12 And 42
May 26, 2025
Related Post
Thank you for visiting our website which covers about 14 Divided By 3 With Remainder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.