Circumference Of A Circle With A Radius Of 3
listenit
Apr 06, 2025 · 5 min read
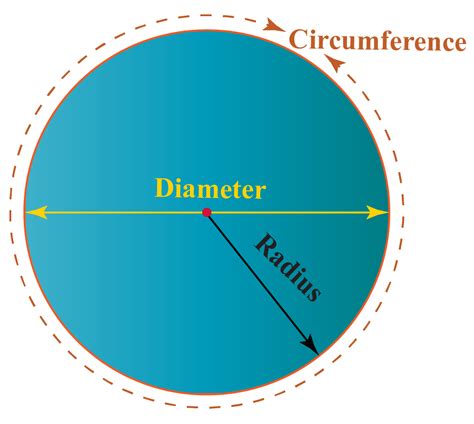
Table of Contents
Circumference of a Circle with a Radius of 3: A Deep Dive into Circular Geometry
The seemingly simple question, "What is the circumference of a circle with a radius of 3?" opens a door to a fascinating world of mathematical concepts, historical context, and practical applications. This exploration will delve deep into understanding the circumference calculation, its implications, and related geometrical principles. We'll journey from the basic formula to more complex applications, solidifying your understanding of this fundamental concept.
Understanding the Basics: Radius, Diameter, and Circumference
Before we calculate the circumference of a circle with a radius of 3, let's define the key terms:
-
Radius: The distance from the center of the circle to any point on the circle. In our case, the radius (r) is 3 units (inches, centimeters, meters – the unit is arbitrary for the calculation itself).
-
Diameter: The distance across the circle passing through the center. The diameter (d) is always twice the radius: d = 2r. Therefore, in our example, the diameter is 2 * 3 = 6 units.
-
Circumference: The distance around the circle. This is the value we're aiming to calculate.
The Formula: Pi and its Significance
The fundamental formula for calculating the circumference (C) of a circle is:
C = 2πr
or, equivalently:
C = πd
Where:
-
C represents the circumference
-
π (pi) is a mathematical constant, approximately equal to 3.14159. Pi represents the ratio of a circle's circumference to its diameter. It's an irrational number, meaning its decimal representation goes on forever without repeating.
-
r represents the radius
-
d represents the diameter
The constant π is crucial to understanding the relationship between a circle's diameter and its circumference. It's a fundamental constant in mathematics and physics, appearing in numerous formulas and equations. Its discovery and approximation throughout history is a testament to the enduring human fascination with circles and their properties.
Calculating the Circumference: A Step-by-Step Guide
Now, let's calculate the circumference of a circle with a radius of 3 using the formula:
C = 2πr
Substituting r = 3, we get:
C = 2 * π * 3 = 6π
This is the exact circumference. To obtain an approximate numerical value, we can use the approximation of π ≈ 3.14159:
C ≈ 6 * 3.14159 ≈ 18.84954 units
Therefore, the circumference of a circle with a radius of 3 units is approximately 18.85 units. Remember that the unit (inches, centimeters, etc.) will be the same as the unit used for the radius.
Beyond the Basics: Exploring Related Concepts
Understanding the circumference of a circle opens up a world of related mathematical concepts:
1. Area of a Circle:
The area (A) of a circle is calculated using the formula:
A = πr²
For a circle with a radius of 3, the area is:
A = π * 3² = 9π ≈ 28.27 square units
2. Sector Area and Arc Length:
A sector is a portion of a circle enclosed by two radii and an arc. The area of a sector and the length of its arc can be calculated using proportions related to the circle's circumference and area.
3. Circumference in Different Coordinate Systems:
The concept of circumference extends beyond Euclidean geometry. In polar coordinates, for example, the circumference is inherently defined by the radial distance and the angle swept.
4. Applications in Real-World Scenarios:
Understanding circumference has numerous practical applications:
-
Engineering and Design: Calculating the circumference is essential in designing circular components, wheels, pipes, and other objects.
-
Construction: It's used in determining the amount of materials needed for circular structures, roads, and pathways.
-
Physics: Circumference plays a vital role in calculations involving circular motion, rotation, and orbital mechanics.
The History of Pi: A Journey Through Time
The understanding and approximation of π have evolved over millennia. Ancient civilizations, including the Babylonians and Egyptians, developed approximations of π through practical measurements. Archimedes, a renowned Greek mathematician, used the method of exhaustion to calculate a remarkably accurate approximation of π between 3.1408 and 3.1429. This involved inscribing and circumscribing regular polygons around a circle and iteratively increasing the number of sides to refine the approximation. Over time, more sophisticated mathematical techniques have enabled the calculation of π to trillions of digits. The ongoing pursuit of calculating π to ever greater precision reflects a persistent human fascination with this fundamental mathematical constant.
Advanced Techniques for Circumference Calculation:
While the basic formula C = 2πr suffices for most applications, more advanced techniques exist for calculating the circumference in complex scenarios:
1. Numerical Integration:
For irregular shapes approximating a circle, numerical integration methods can be applied to estimate the circumference. These methods involve breaking down the curve into small segments and approximating the length of each segment.
2. Calculus:
Calculus provides powerful tools for determining the circumference of curves defined by functions. Arc length calculations, using integration, enable the precise determination of circumference for complex shapes.
3. Computer Algorithms:
Sophisticated computer algorithms are used to calculate π to trillions of digits, far beyond what is needed for practical purposes but showcasing the power of computational methods.
Conclusion: The Enduring Relevance of Circular Geometry
The seemingly straightforward calculation of the circumference of a circle with a radius of 3, yielding a result of approximately 18.85 units, unveils a profound connection to fundamental mathematical concepts, historical discoveries, and practical applications. From the ancient civilizations who first approximated π to the modern-day advancements in computational power, the exploration of circular geometry remains an area of ongoing fascination and investigation. Understanding the circumference is not just about a simple calculation; it's about grasping a fundamental aspect of geometry and its widespread relevance in various fields of science and engineering. The journey from the basic formula to advanced mathematical techniques highlights the depth and complexity inherent in this seemingly simple concept. The enduring relevance of circular geometry and the constant pi underscores the power of mathematical principles in shaping our understanding of the world around us.
Latest Posts
Latest Posts
-
6 To The Power Of 7
Apr 07, 2025
-
Greatest Common Factor 12 And 18
Apr 07, 2025
-
Write A Linear Function X With The Given Values
Apr 07, 2025
-
Graph Of X 2 Y 2 0
Apr 07, 2025
-
Why Is Cosx An Even Function
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Circumference Of A Circle With A Radius Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
