Greatest Common Factor 12 And 18
listenit
Apr 07, 2025 · 5 min read
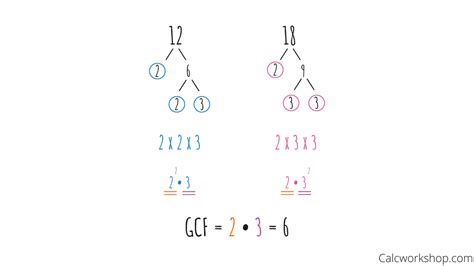
Table of Contents
Greatest Common Factor of 12 and 18: A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but it forms the bedrock of many important concepts in mathematics, from simplifying fractions to solving algebraic equations. This article delves deep into finding the GCF of 12 and 18, exploring various methods, their applications, and the underlying mathematical principles. We'll go beyond just finding the answer; we'll understand why the methods work and how they relate to broader mathematical concepts.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides evenly into two or more numbers without leaving a remainder. Think of it as the biggest shared factor amongst the numbers. For example, the GCF of 12 and 18 is the largest number that can divide both 12 and 18 perfectly.
Why is the GCF Important?
The GCF is a fundamental concept with numerous applications across various mathematical fields:
-
Simplifying Fractions: The GCF is crucial for reducing fractions to their simplest form. By dividing both the numerator and denominator by their GCF, you obtain an equivalent fraction with smaller numbers, making it easier to understand and work with.
-
Algebraic Expressions: Finding the GCF helps simplify algebraic expressions by factoring out common terms. This simplification is essential for solving equations and simplifying more complex mathematical expressions.
-
Number Theory: GCF plays a vital role in number theory, the study of integers and their properties. It forms the basis for many advanced concepts and theorems.
-
Real-world Applications: From dividing objects evenly to solving problems involving ratios and proportions, understanding the GCF has practical applications in everyday life.
Methods for Finding the GCF of 12 and 18
Several methods can efficiently determine the GCF of 12 and 18. We will explore the most common approaches:
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest factor common to both.
Factors of 12: 1, 2, 3, 4, 6, 12 Factors of 18: 1, 2, 3, 6, 9, 18
The common factors are 1, 2, 3, and 6. Therefore, the GCF of 12 and 18 is 6.
This method is straightforward for smaller numbers but can become cumbersome for larger numbers with many factors.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
Prime Factorization of 12: 2² x 3 Prime Factorization of 18: 2 x 3²
The common prime factors are 2 and 3. The lowest power of 2 is 2¹, and the lowest power of 3 is 3¹. Multiplying these together: 2 x 3 = 6. Therefore, the GCF of 12 and 18 is 6.
3. Euclidean Algorithm
The Euclidean Algorithm is an efficient method, particularly useful for larger numbers. It's based on repeated application of the division algorithm.
- Divide the larger number (18) by the smaller number (12): 18 ÷ 12 = 1 with a remainder of 6.
- Replace the larger number with the smaller number (12) and the smaller number with the remainder (6): Now we find the GCF of 12 and 6.
- Repeat the process: 12 ÷ 6 = 2 with a remainder of 0.
- The GCF is the last non-zero remainder. In this case, the last non-zero remainder is 6. Therefore, the GCF of 12 and 18 is 6.
Applications of the GCF: Real-world Examples
The GCF's applications extend beyond theoretical mathematics. Let's explore some real-world examples:
1. Dividing Objects Evenly
Imagine you have 12 apples and 18 oranges, and you want to divide them into identical groups with the same number of apples and oranges in each group. The GCF (6) tells you that you can create 6 identical groups, each containing 2 apples and 3 oranges.
2. Simplifying Fractions
Consider the fraction 18/12. To simplify this fraction, we find the GCF of 18 and 12, which is 6. Dividing both the numerator and denominator by 6 gives us the simplified fraction 3/2.
3. Ratio and Proportion Problems
Let's say a recipe calls for 12 cups of flour and 18 cups of sugar. To maintain the same ratio, but use smaller amounts, we can divide both quantities by their GCF (6). This gives us a simplified ratio of 2 cups of flour to 3 cups of sugar.
GCF and Least Common Multiple (LCM)
The GCF is closely related to the least common multiple (LCM). The LCM is the smallest number that is a multiple of both numbers. For 12 and 18:
Multiples of 12: 12, 24, 36, 48, 60... Multiples of 18: 18, 36, 54, 72...
The smallest common multiple is 36. There's a useful relationship between the GCF and LCM:
(GCF(a, b) x LCM(a, b)) = a x b
In our case: (6 x 36) = 12 x 18 = 216. This formula provides a quick way to find the LCM if you already know the GCF, or vice-versa.
Advanced Concepts and Further Exploration
While we've focused on the GCF of 12 and 18, the principles extend to more complex scenarios:
-
Finding the GCF of more than two numbers: The same methods (prime factorization and the Euclidean algorithm) can be extended to find the GCF of three or more numbers.
-
Applications in cryptography: The GCF plays a role in certain cryptographic algorithms, particularly those related to modular arithmetic.
-
Abstract Algebra: The concept of GCF extends to more abstract mathematical structures, such as rings and ideals.
Conclusion
Finding the greatest common factor of 12 and 18, seemingly a simple task, reveals a rich tapestry of mathematical concepts and practical applications. Understanding the different methods, their underlying principles, and their connections to other mathematical ideas provides a solid foundation for further exploration in number theory and beyond. Mastering the GCF is not merely about performing calculations; it's about grasping the fundamental relationships between numbers and developing problem-solving skills applicable in numerous contexts. The exploration of the GCF offers a rewarding journey into the heart of mathematics, illustrating the power and elegance of seemingly simple concepts.
Latest Posts
Latest Posts
-
What Is The Charge Of Calcium Ion
Apr 09, 2025
-
What Holds Molecules Of Fluorine Together
Apr 09, 2025
-
How Many Lbs Is 96 Oz
Apr 09, 2025
-
What Type Of Bond Is Formed When Electrons Are Shared
Apr 09, 2025
-
Is Burning Paper A Physical Or Chemical Change
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about Greatest Common Factor 12 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.