Area Of A Circle 9 Inch Diameter
listenit
Mar 31, 2025 · 5 min read
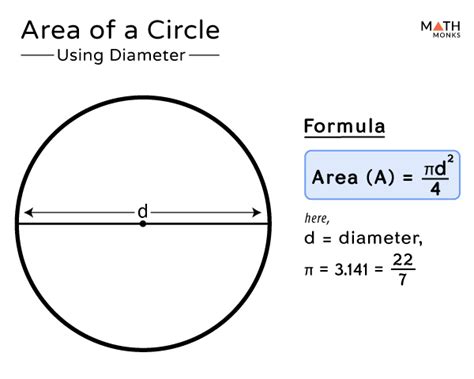
Table of Contents
Area of a Circle: A 9-Inch Diameter Deep Dive
The seemingly simple question, "What is the area of a circle with a 9-inch diameter?" opens a door to a fascinating exploration of geometry, mathematical formulas, and their real-world applications. While the calculation itself is straightforward, understanding the underlying principles and the broader implications of the area of a circle are crucial for various fields, from engineering and design to everyday problem-solving. This comprehensive guide delves into the specifics of calculating the area of a 9-inch diameter circle, expands on the concepts involved, and highlights practical applications.
Understanding the Formula: Pi and the Power of Circles
The area of any circle is calculated using a fundamental formula: Area = πr², where:
- A represents the area of the circle.
- π (pi) is a mathematical constant, approximately equal to 3.14159. Pi represents the ratio of a circle's circumference to its diameter and is an irrational number, meaning its decimal representation goes on forever without repeating.
- r represents the radius of the circle, which is half the diameter.
This formula encapsulates the elegant relationship between a circle's radius and its area. A larger radius inevitably leads to a larger area, and this relationship is precisely defined by the constant pi.
Calculating the Area of a 9-Inch Diameter Circle
Since the diameter of our circle is 9 inches, the radius (r) is half of that, which is 4.5 inches. Now, we can substitute the values into the formula:
Area = π * (4.5 inches)²
Area = π * 20.25 square inches
Using the approximation of π ≈ 3.14159, we get:
Area ≈ 3.14159 * 20.25 square inches
Area ≈ 63.617 square inches
Therefore, the area of a circle with a 9-inch diameter is approximately 63.62 square inches. We round to two decimal places for practical purposes.
Beyond the Calculation: Understanding the Significance of Pi
Pi's significance extends far beyond calculating the area of a circle. It's a fundamental constant in mathematics and physics, appearing in countless formulas and equations related to circles, spheres, and other curved shapes. Its irrational nature, the fact it can't be expressed as a simple fraction, makes it a fascinating subject of mathematical study and exploration. Understanding pi's role in calculating circular areas provides a glimpse into its broader importance in mathematics and science.
Pi's Historical Significance and Mathematical Depth
The pursuit of pi's value has captivated mathematicians for millennia. Ancient civilizations, including the Babylonians and Egyptians, made estimations of pi, albeit with less accuracy than modern approximations. The symbol 'π' itself was introduced in the 18th century, solidifying its place in mathematical notation. The ongoing exploration of pi, and the search for more accurate estimations, continues to drive mathematical discovery and computation.
Practical Applications: Circles in the Real World
The ability to calculate the area of a circle has numerous real-world applications across diverse fields. Understanding this concept is vital in:
Engineering and Design
-
Designing circular components: Engineers use this calculation to determine the material needed for parts such as pipes, gears, and other circular components. Accurate area calculations are crucial for optimizing material usage and minimizing waste.
-
Civil Engineering: Calculating the area of circular structures like water tanks, reservoirs, and even roundabout intersections is essential for planning and design. This ensures efficient capacity and resource allocation.
-
Mechanical Engineering: Determining the surface area of pistons, wheels, and other rotating components is critical for understanding friction, heat transfer, and other mechanical properties.
Manufacturing and Production
-
Cutting and shaping materials: Manufacturers need precise area calculations to determine the amount of material needed for cutting circles from sheets or rolls of material, minimizing waste and optimizing production efficiency.
-
Packaging and containers: Designing circular containers, like cans or lids, requires accurate area calculations to ensure correct dimensions and optimal material usage.
Everyday Applications
-
Gardening and Landscaping: Calculating the area of a circular flower bed or garden patch helps determine the amount of soil, fertilizer, or mulch needed.
-
Cooking and Baking: Understanding circular areas can aid in determining the appropriate amount of ingredients for recipes involving circular baking pans or dishes.
-
Arts and Crafts: Many crafting projects involve circular shapes, and precise area calculations are often necessary for material estimation and design planning.
Expanding the Concept: Area of Sectors and Segments
The concept of calculating the area of a circle extends to its parts:
-
Sector: A sector is a portion of a circle enclosed by two radii and an arc. The area of a sector is a fraction of the total area of the circle, determined by the angle of the sector.
-
Segment: A segment is the area enclosed between a chord and an arc of a circle. Calculating the area of a segment involves more complex calculations, often requiring trigonometric functions.
Advanced Applications and Further Exploration
Beyond the basic calculation, understanding the area of a circle forms the foundation for more advanced concepts, including:
-
Calculus: The concept of area is deeply ingrained in integral calculus, where the area under curves is often calculated using integration techniques.
-
Solid Geometry: The area of a circle is crucial for calculating the surface area and volume of three-dimensional shapes, like cylinders, cones, and spheres.
-
Probability and Statistics: Circular areas play a role in probability calculations, particularly those involving random points within a circle.
-
Physics: Circular areas appear frequently in physics, particularly in calculations related to motion, force, and energy.
Conclusion: The Enduring Importance of Circular Area Calculations
The calculation of the area of a circle, even for a seemingly simple 9-inch diameter example, reveals a rich tapestry of mathematical concepts and real-world applications. From the fundamental constant pi to its diverse applications in engineering, design, manufacturing, and even everyday life, understanding this calculation empowers us to solve problems, optimize processes, and appreciate the elegance and utility of mathematics. The seemingly simple formula, Area = πr², holds within it a universe of mathematical depth and practical significance.
Latest Posts
Latest Posts
-
What Is The Lcm For 6 And 10
Apr 02, 2025
-
Which Organelles Supply Energy To The Cell
Apr 02, 2025
-
Why Is Density A Physical Property
Apr 02, 2025
-
Is Koh A Base Or Acid
Apr 02, 2025
-
Why Did Small States Object To The Virginia Plan
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Area Of A Circle 9 Inch Diameter . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
