Are Frequency And Wavelength Directly Proportional
listenit
Mar 30, 2025 · 5 min read
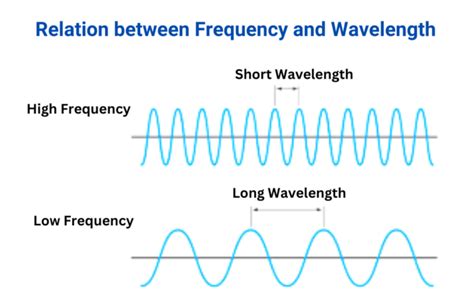
Table of Contents
Are Frequency and Wavelength Directly Proportional? A Deep Dive into the Relationship
The relationship between frequency and wavelength is a cornerstone of physics, particularly in the study of waves, including light, sound, and electromagnetic radiation. A common question that arises is: are frequency and wavelength directly proportional? The simple answer is no, they are inversely proportional. This seemingly simple concept has profound implications across various scientific disciplines. This article will delve into the intricacies of this relationship, exploring its mathematical representation, providing real-world examples, and addressing common misconceptions.
Understanding the Basics: Frequency and Wavelength
Before examining their relationship, let's define the key terms:
Frequency (f): This refers to the number of complete wave cycles that pass a fixed point in one second. It's measured in Hertz (Hz), where 1 Hz equals one cycle per second. Think of it as the rate of oscillation or vibration. A higher frequency means more cycles per second, indicating a faster oscillation.
Wavelength (λ): This represents the distance between two consecutive corresponding points on a wave, such as two adjacent crests or troughs. It's usually measured in meters (m), nanometers (nm), or other units of length depending on the type of wave. A longer wavelength implies a greater distance between these points.
The Inverse Relationship: Why They Are Not Directly Proportional
The fundamental relationship between frequency (f) and wavelength (λ) is governed by the following equation:
v = fλ
where:
- v represents the velocity or speed of the wave (constant for a given medium).
This equation reveals the inverse relationship: if the frequency (f) increases, the wavelength (λ) must decrease to maintain a constant velocity (v), and vice versa. This is why they are inversely proportional, not directly proportional. A larger frequency means a shorter wavelength, and a smaller frequency means a longer wavelength. The constant velocity acts as a constraint, ensuring that the product of frequency and wavelength remains constant for a specific medium.
Understanding the Constant Velocity (v)
The velocity (v) in the equation is crucial. For a given medium (e.g., air, water, vacuum), the speed of a wave is constant. This constant velocity differs for different mediums. For example:
- Light in a vacuum: The speed of light (c) is approximately 3 x 10⁸ meters per second (m/s), a fundamental constant in physics.
- Sound in air: The speed of sound in air is approximately 343 m/s at room temperature, but it varies with temperature and humidity.
This constant velocity is what dictates the inverse relationship between frequency and wavelength. The medium determines the speed; the frequency and wavelength adjust accordingly to satisfy the equation.
Real-World Examples Illustrating the Inverse Proportionality
Let's consider some real-world examples to solidify our understanding:
1. Electromagnetic Spectrum:
The electromagnetic spectrum encompasses a vast range of frequencies and wavelengths, from radio waves with long wavelengths and low frequencies to gamma rays with short wavelengths and high frequencies. All these waves travel at the speed of light in a vacuum. This wide spectrum perfectly illustrates the inverse relationship: as frequency increases, wavelength decreases, and vice-versa, all while maintaining the constant speed of light.
2. Sound Waves:
Consider a musical instrument. High-pitched notes correspond to high-frequency sound waves with shorter wavelengths. Low-pitched notes, on the other hand, correspond to low-frequency sound waves with longer wavelengths. The speed of sound in air remains relatively constant (barring changes in temperature and humidity), thus demonstrating the inverse proportionality.
3. Water Waves:
Observe the waves in the ocean. Waves with higher frequencies (more waves passing a point per second) tend to have shorter wavelengths, while waves with lower frequencies (fewer waves passing a point per second) have longer wavelengths. The speed of the water wave depends on factors like water depth and current, but for a given set of conditions, the inverse proportionality holds.
Addressing Common Misconceptions
Several misconceptions often surround the relationship between frequency and wavelength:
-
Confusing Direct and Inverse Proportionality: Many students initially mistake the relationship for a direct proportion, perhaps because both frequency and wavelength are properties of the wave. However, the constant velocity acts as a constraint, enforcing the inverse relationship.
-
Ignoring the Medium: It's crucial to remember that the velocity (v) is medium-dependent. The same frequency will result in different wavelengths when the wave travels through different mediums. The equation v = fλ must always be considered in context.
-
Assuming Linearity: The relationship is inversely proportional, not necessarily linearly proportional. While the equation v = fλ represents a linear relationship between v, f, and λ, the focus is on the inverse relationship between f and λ when v is held constant.
Mathematical Demonstrations of the Inverse Relationship
Let's consider a few mathematical scenarios to highlight the inverse proportionality:
Scenario 1: A wave has a frequency of 10 Hz and a wavelength of 1 meter in a given medium. The velocity is 10 m/s (v = fλ = 10 Hz * 1 m = 10 m/s). If the frequency increases to 20 Hz, and the velocity remains constant at 10 m/s, then the wavelength must decrease to 0.5 meters (λ = v/f = 10 m/s / 20 Hz = 0.5 m).
Scenario 2: A light wave in a vacuum has a frequency of 5 x 10¹⁴ Hz. Using the speed of light (c ≈ 3 x 10⁸ m/s), we can calculate its wavelength: λ = c/f ≈ (3 x 10⁸ m/s) / (5 x 10¹⁴ Hz) ≈ 6 x 10⁻⁷ m or 600 nm (this falls within the visible light spectrum). If the frequency were doubled to 10 x 10¹⁴ Hz, the wavelength would halve to 300 nm (ultraviolet range).
Conclusion: The Importance of Understanding Inverse Proportionality
The inverse relationship between frequency and wavelength is a fundamental concept in wave physics. Understanding this relationship is critical for comprehending various phenomena, from the behavior of light and sound to the workings of technologies like radio communication and medical imaging. By grasping the underlying principles and overcoming common misconceptions, we can better appreciate the elegant and powerful relationship between these two fundamental wave properties. Remembering the equation v = fλ and the crucial role of the constant velocity (v) for a given medium are key to a thorough understanding. The inverse proportionality, not a direct one, governs this crucial aspect of wave behavior.
Latest Posts
Latest Posts
-
How Many Electrons Does O Have
Apr 01, 2025
-
Solve This Inequality J 4 8 4
Apr 01, 2025
-
What Happens When You Cut A Magnet In Half
Apr 01, 2025
-
How Does An Ion Differ From An Atom
Apr 01, 2025
-
A Solution In Which Water Is The Solvent
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Are Frequency And Wavelength Directly Proportional . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
