A Rhombus Is A Regular Polygon
listenit
Mar 28, 2025 · 4 min read
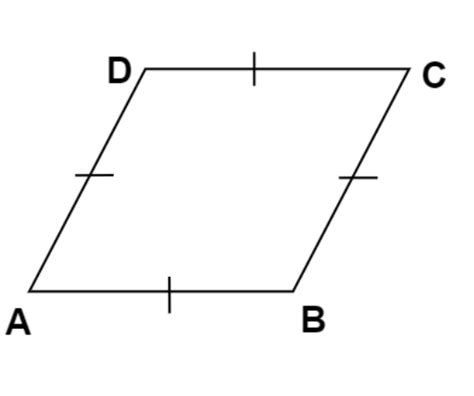
Table of Contents
Is a Rhombus a Regular Polygon? Exploring the Properties of Quadrilaterals
The question, "Is a rhombus a regular polygon?" might seem straightforward, but delving into the geometric definitions reveals a nuanced answer. Understanding the properties of both rhombuses and regular polygons is crucial to clarifying this relationship. This article will thoroughly explore the characteristics of each shape, compare their defining features, and ultimately answer the central question while enriching your understanding of geometric concepts.
Defining a Rhombus: A Deep Dive into its Properties
A rhombus, a type of quadrilateral, is defined by its four sides, all of which are equal in length. This property is the cornerstone of its identity. However, the angles within a rhombus are not necessarily equal. Let's explore some key characteristics:
Key Properties of a Rhombus:
- Equilateral Sides: This is the defining characteristic. All four sides are congruent (equal in length).
- Opposite Angles are Equal: The angles opposite each other within the rhombus are equal in measure.
- Consecutive Angles are Supplementary: Any two angles that share a side (consecutive angles) add up to 180 degrees.
- Diagonals Bisect Each Other: The diagonals of a rhombus intersect at a point, and each diagonal bisects (cuts in half) the other.
- Diagonals are Perpendicular: The diagonals intersect at a right angle (90 degrees).
- Diagonals Bisect Angles: Each diagonal bisects a pair of opposite angles.
These properties distinguish a rhombus from other quadrilaterals like squares, rectangles, parallelograms, and trapezoids. While it shares some similarities with these shapes, the unique combination of equal sides and potentially unequal angles sets it apart. Understanding these properties is fundamental to answering whether it qualifies as a regular polygon.
Understanding Regular Polygons: A Comprehensive Overview
A regular polygon is a polygon that exhibits both equilateral and equiangular characteristics. This means that:
Essential Properties of a Regular Polygon:
- Equilateral: All sides are of equal length.
- Equiangular: All angles are of equal measure.
This combination of properties is crucial. A polygon might be equilateral without being equiangular (like a rhombus), or it could be equiangular without being equilateral (like certain rectangles). Only when both conditions are met can a polygon be classified as regular.
Comparing Rhombuses and Regular Polygons: Unveiling the Discrepancy
Now, let's directly compare the properties of a rhombus to those of a regular polygon. While a rhombus possesses equilateral sides (all sides are equal), it does not necessarily possess equiangular properties (all angles are equal). This is the critical difference.
Rhombus: Equal sides, potentially unequal angles.
Regular Polygon: Equal sides AND equal angles.
Because a rhombus can have unequal angles, it fails to satisfy the complete definition of a regular polygon. Therefore, the answer is definitively no, a rhombus is not a regular polygon in the strictest sense of the geometric definition.
Special Case: The Square – A Regular Rhombus
A fascinating exception to this rule is the square. A square is a special type of rhombus where all angles are also equal (90 degrees). In this specific instance, a square satisfies both the equilateral and equiangular conditions required for a regular polygon. Therefore, a square is a regular polygon and also a rhombus. This highlights the hierarchical relationship between these shapes: all squares are rhombuses, but not all rhombuses are squares.
Exploring Other Quadrilaterals and Their Relationship to Regular Polygons
Let’s briefly consider other quadrilaterals:
- Rectangles: These possess equal angles (90 degrees) but not necessarily equal sides. They are not regular polygons.
- Parallelograms: These have opposite sides equal and opposite angles equal, but not necessarily all sides and angles equal. They are not regular polygons.
- Trapezoids: These only have one pair of parallel sides. They are not regular polygons.
Only the square, a specific type of rhombus, fulfills the conditions to be classified as a regular polygon amongst these quadrilaterals.
Practical Applications and Real-World Examples
Understanding the difference between a rhombus and a regular polygon is not just an academic exercise. These shapes have practical applications in various fields:
- Engineering: Structural designs often utilize the properties of rhombuses and squares (regular rhombuses) for stability and load distribution.
- Architecture: Building structures, tiling patterns, and architectural designs often incorporate these shapes for aesthetic and functional purposes.
- Art and Design: Rhombuses and squares are frequently found in artwork, graphic design, and textile patterns.
- Crystallography: The structure of certain crystals can be modeled using rhombic and square lattices.
Conclusion: A Clear Distinction and Further Exploration
In conclusion, a rhombus is not a regular polygon because while it satisfies the equilateral condition (equal sides), it does not always fulfill the equiangular condition (equal angles). The square, a special case of the rhombus, is the only rhombus that is also a regular polygon. This exploration highlights the importance of precise geometric definitions and the nuanced relationships between different geometric shapes. Further exploration into other polygons and their properties can enrich your understanding of geometry and its applications in the real world. Understanding these concepts enhances your ability to analyze shapes, solve problems, and appreciate the beauty and complexity of geometric forms. The key takeaway remains: the critical distinction lies in the necessity of both equal sides and equal angles for a polygon to be classified as regular.
Latest Posts
Latest Posts
-
What Is The Name Of This Hydrocarbon
Mar 31, 2025
-
Columns Of Periodic Table Are Called
Mar 31, 2025
-
Difference Between Animal Mitosis And Plant Mitosis
Mar 31, 2025
-
What Is Half Of One And A Half Teaspoons
Mar 31, 2025
-
What Is 4 12 In Simplest Form
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about A Rhombus Is A Regular Polygon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
