A Quadrilateral With Two Right Angles
listenit
Apr 03, 2025 · 5 min read
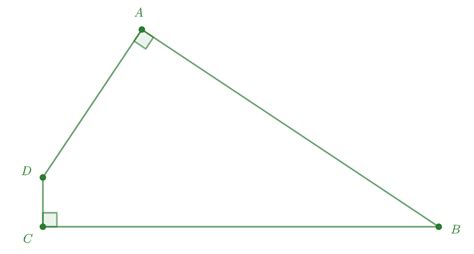
Table of Contents
A Quadrilateral with Two Right Angles: Exploring its Properties and Types
A quadrilateral, a polygon with four sides and four angles, presents a rich landscape for geometric exploration. When we introduce the constraint of two right angles, the possibilities narrow but still offer fascinating variations and properties. This article delves deep into the world of quadrilaterals possessing two right angles, exploring their characteristics, classifications, and applications. We will uncover the unique features that distinguish them and understand how they relate to other more familiar quadrilaterals.
Understanding the Basics: Properties of Quadrilaterals with Two Right Angles
Before we dive into specifics, let's establish a foundational understanding. A quadrilateral with exactly two right angles possesses several inherent properties:
-
Sum of Angles: Like all quadrilaterals, the sum of its interior angles always equals 360 degrees. This fundamental property helps in determining the measures of the remaining angles.
-
Non-parallel Sides: Crucially, the presence of only two right angles precludes the possibility of the quadrilateral being a rectangle or square. These shapes require all four angles to be right angles. This means at least one pair of opposite sides will not be parallel.
-
Variable Shape: The shape and properties of the quadrilateral are highly variable depending on the arrangement and lengths of the sides. This means we can't definitively say much about the lengths of sides or other angles without additional information.
Classifying Quadrilaterals with Two Right Angles
The absence of a single, overarching name for this category of quadrilaterals indicates the diversity within. They are not a formally defined geometric shape in the same way as rectangles or squares. However, we can categorize them based on additional characteristics:
1. Cyclic Quadrilaterals with Two Right Angles
A cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. If a quadrilateral has two right angles, it can be cyclic under certain conditions. Let's consider this scenario:
-
Opposite Angles: In a cyclic quadrilateral, opposite angles are supplementary (they add up to 180 degrees). If two angles are right angles (90 degrees each), their opposite angles must also be 90 degrees to satisfy the 360-degree sum. Therefore, this specific type of quadrilateral is also a cyclic quadrilateral.
-
Diameter: The line segment connecting the vertices of the two right angles acts as the diameter of the circle that circumscribes the quadrilateral. This is a direct consequence of Thales' theorem, which states that any angle inscribed in a semicircle is a right angle.
2. Non-Cyclic Quadrilaterals with Two Right Angles
Many quadrilaterals with two right angles are not cyclic. They fail to meet the condition of opposite angles being supplementary. Their shape and properties are even more diverse and depend heavily on the arrangement of the sides and angles.
Exploring Specific Cases and Their Properties
Let's examine some examples to illustrate the diverse nature of quadrilaterals with two right angles:
Case 1: Two Adjacent Right Angles
Imagine a quadrilateral where two right angles share a common side. This immediately suggests the possibility of a shape resembling an "L" shape.
-
Properties: The other two angles will be supplementary (they will add up to 180 degrees) to fulfill the 360-degree sum for the interior angles. However, there are no other constraints on the lengths of the sides. The shape can range from a near-rectangle (where the other two angles are close to 90 degrees) to a very elongated "L" shape.
-
Applications: This shape could represent various architectural elements, components in engineering designs, or patterns in art and design.
Case 2: Two Opposite Right Angles
This is the case of the cyclic quadrilateral mentioned earlier. This configuration is far more constrained than Case 1.
-
Properties: As we already established, the opposite angles are also right angles, resulting in a cyclic quadrilateral inscribed within a circle. The line segment joining the two right angle vertices forms the diameter of the circle.
-
Applications: This configuration finds applications in various geometric constructions and proofs. Its symmetry lends itself to simpler calculations and analysis.
Using Coordinates to Analyze Quadrilaterals with Two Right Angles
Coordinate geometry offers a powerful tool for analyzing these quadrilaterals. By assigning coordinates to the vertices, we can precisely define their shape and calculate properties like area and side lengths.
Let's consider a simple example: Suppose we have a quadrilateral with vertices A(0,0), B(a,0), C(a,b), and D(0,c). If angles A and B are right angles, this defines a quadrilateral with two adjacent right angles. Using distance formula and slope calculations, you could analyze the lengths of the sides, the measures of angles C and D and the area of this quadrilateral. Different coordinates will generate various instances of quadrilaterals with two right angles allowing for a detailed comparative analysis.
Further Investigations and Related Concepts
The study of quadrilaterals with two right angles opens doors to various deeper explorations:
-
Isosceles Trapezoids: While not all quadrilaterals with two right angles are isosceles trapezoids, an isosceles trapezoid is a specific case where the non-parallel sides are equal in length and each pair of adjacent angles are supplementary.
-
Area Calculation: Developing general formulas for the area of a quadrilateral with two right angles is challenging due to its varied shapes. Different approaches using coordinates, triangles, and other geometric techniques will provide a path toward solving such a problem.
-
Advanced Geometric Properties: Investigating properties related to diagonals, angles bisectors, and other geometric elements can lead to a more profound understanding.
Conclusion: A World of Shapes Beyond the Familiar
Quadrilaterals with two right angles represent a diverse and fascinating subset of quadrilaterals, extending beyond the commonly studied shapes like rectangles and squares. Their properties, varied shapes, and the interplay of geometric principles make them a rewarding area for study. By systematically exploring their characteristics and employing various analytical tools, we can unveil the rich mathematical structures hidden within these seemingly simple polygons. This opens avenues for further exploration in geometry, offering opportunities to develop a deeper appreciation for the elegance and complexity of geometric shapes and their properties. Understanding these shapes allows for a more thorough understanding of geometry, its applications, and how to apply different geometric methods in solving real world problems. The applications expand to various fields such as architecture, engineering, art, and even computer graphics, where such shapes form the basis of various designs and constructions.
Latest Posts
Latest Posts
-
How Does An Igneous Rock Turn Into A Metamorphic Rock
Apr 04, 2025
-
What Is The Lcm Of 6 And 5
Apr 04, 2025
-
Which One Increases Number Of Collisions Between The Reactants
Apr 04, 2025
-
How Many Feet In 1 2 Miles
Apr 04, 2025
-
What Is 3 4 Of A Pound
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about A Quadrilateral With Two Right Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
