A 2 B 2 C 2 Solve For B
listenit
May 24, 2025 · 4 min read
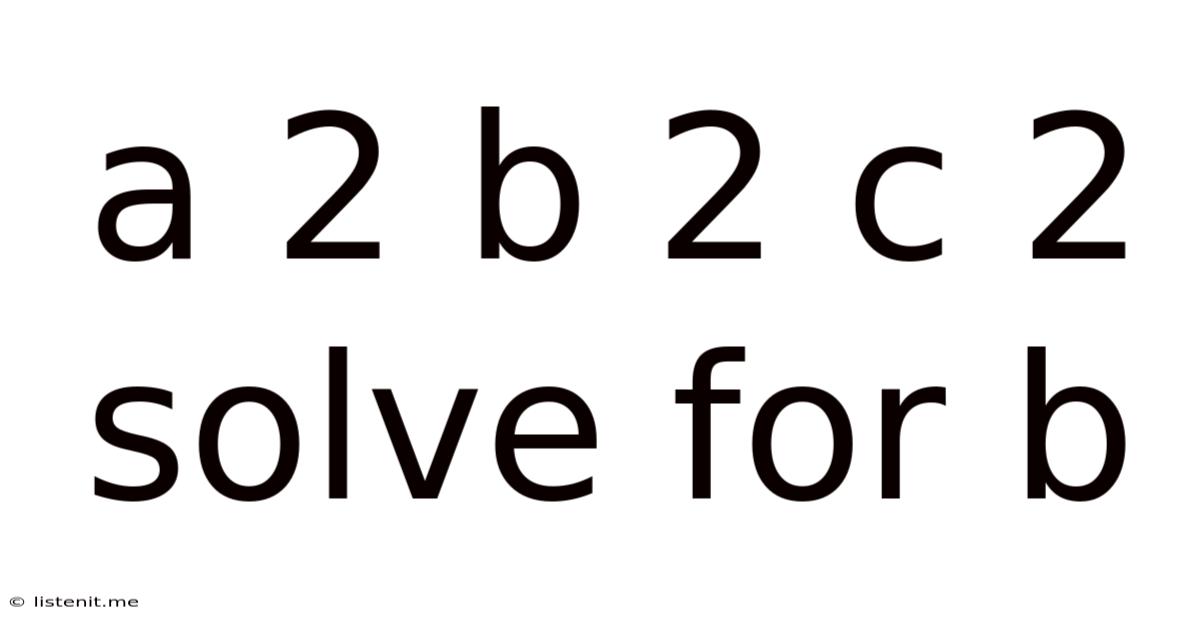
Table of Contents
Solving for 'b': A Comprehensive Guide to the Equation a² + b² = c²
The equation a² + b² = c² is a cornerstone of geometry and mathematics, famously known as the Pythagorean theorem. While often used to find the hypotenuse (c) of a right-angled triangle given the lengths of the other two sides (a and b), it's equally valuable in solving for any of the three variables if the other two are known. This article will delve into the process of solving for 'b' in the equation a² + b² = c², providing a comprehensive guide with various examples and considerations.
Understanding the Pythagorean Theorem
Before jumping into the solution, let's revisit the fundamentals. The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (called legs or cathetus). This relationship is expressed mathematically as:
a² + b² = c²
Where:
- a represents the length of one leg of the right-angled triangle.
- b represents the length of the other leg of the right-angled triangle.
- c represents the length of the hypotenuse (the longest side).
Solving for 'b'
To solve for 'b', we need to isolate 'b' on one side of the equation. This involves a series of algebraic manipulations:
-
Subtract a² from both sides: This removes 'a²' from the left side, leaving only b²:
b² = c² - a²
-
Take the square root of both sides: This eliminates the square on 'b', giving us the value of 'b':
b = √(c² - a²)
Important Note: The result will always be positive because length is always positive. However, remember that the square root of a number can have both a positive and a negative solution. Since we are dealing with lengths, we only consider the positive solution.
Practical Examples: Solving for 'b' with Different Values
Let's illustrate the process with several examples, demonstrating how to apply the formula and handle different scenarios:
Example 1: Simple Calculation
Let's assume a = 3 and c = 5. We want to find the value of b.
-
Substitute the values into the formula: b = √(c² - a²) = √(5² - 3²)
-
Calculate the squares: b = √(25 - 9) = √16
-
Find the square root: b = 4
Therefore, in this right-angled triangle with one leg of length 3 and hypotenuse of length 5, the other leg has a length of 4.
Example 2: Dealing with Decimals
Let's consider a = 2.5 and c = 6. We'll use the same formula:
-
Substitute the values: b = √(6² - 2.5²) = √(36 - 6.25)
-
Calculate the difference: b = √29.75
-
Find the square root (using a calculator): b ≈ 5.45
This example demonstrates that the formula works equally well with decimal values.
Example 3: Working with Larger Numbers
Let's use larger numbers to showcase the power of the formula: a = 12 and c = 15.
-
Substitute the values: b = √(15² - 12²) = √(225 - 144)
-
Calculate the difference: b = √81
-
Find the square root: b = 9
This example highlights that even with larger numbers, the process remains straightforward.
Error Handling and Considerations
While the formula is straightforward, there are certain scenarios to be mindful of:
-
c² < a²: If the square of the hypotenuse (c²) is less than the square of one leg (a²), the result inside the square root will be negative. This is impossible in the context of real-world lengths, indicating an error in the input values. The hypotenuse must always be the longest side of a right-angled triangle.
-
Rounding Errors: When dealing with decimal values, be aware of potential rounding errors. Using a calculator with sufficient precision is recommended to minimize inaccuracies.
-
Units of Measurement: Always ensure that the units of measurement (e.g., centimeters, meters, inches) are consistent for all sides (a, b, and c) to ensure accurate calculations.
Applications of Solving for 'b'
The ability to solve for 'b' in the Pythagorean theorem has far-reaching applications across various fields:
-
Engineering and Construction: Calculating distances, determining structural integrity, and designing building layouts.
-
Surveying and Mapping: Determining distances and elevations, creating accurate maps and plans.
-
Navigation: Calculating distances and directions, especially in scenarios involving right-angled triangles.
-
Computer Graphics: Creating realistic 3D models and simulations, accurately calculating distances and positions of objects.
-
Physics: Solving problems related to vectors, forces, and motion, where right-angled triangles are frequently encountered.
Beyond the Basics: Extending the Understanding
While the focus has been on solving for 'b', the same principles can be applied to solve for 'a' or 'c' in the Pythagorean theorem:
-
Solving for 'a': a = √(c² - b²)
-
Solving for 'c': c = √(a² + b²)
Understanding how to manipulate this fundamental equation opens up a world of problem-solving possibilities in various fields.
Conclusion
Solving for 'b' in the equation a² + b² = c² is a fundamental skill in mathematics and has practical implications in numerous fields. By mastering this process, and understanding the associated considerations and potential error sources, you empower yourself with a valuable tool for tackling various geometric and mathematical challenges. Remember to always double-check your work and ensure that your inputs are consistent and valid to obtain accurate and reliable results. This comprehensive guide provides a solid foundation for understanding and applying this essential mathematical concept.
Latest Posts
Latest Posts
-
What Is 5 Percent Of 60
May 24, 2025
-
30 Days From December 16 2024
May 24, 2025
-
Find The Total Surface Area Of The Figure Below
May 24, 2025
-
What Time Is It In 30 Min
May 24, 2025
-
What Is 100 Divided By 8
May 24, 2025
Related Post
Thank you for visiting our website which covers about A 2 B 2 C 2 Solve For B . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.