What Is 5 Percent Of 60
listenit
May 24, 2025 · 4 min read
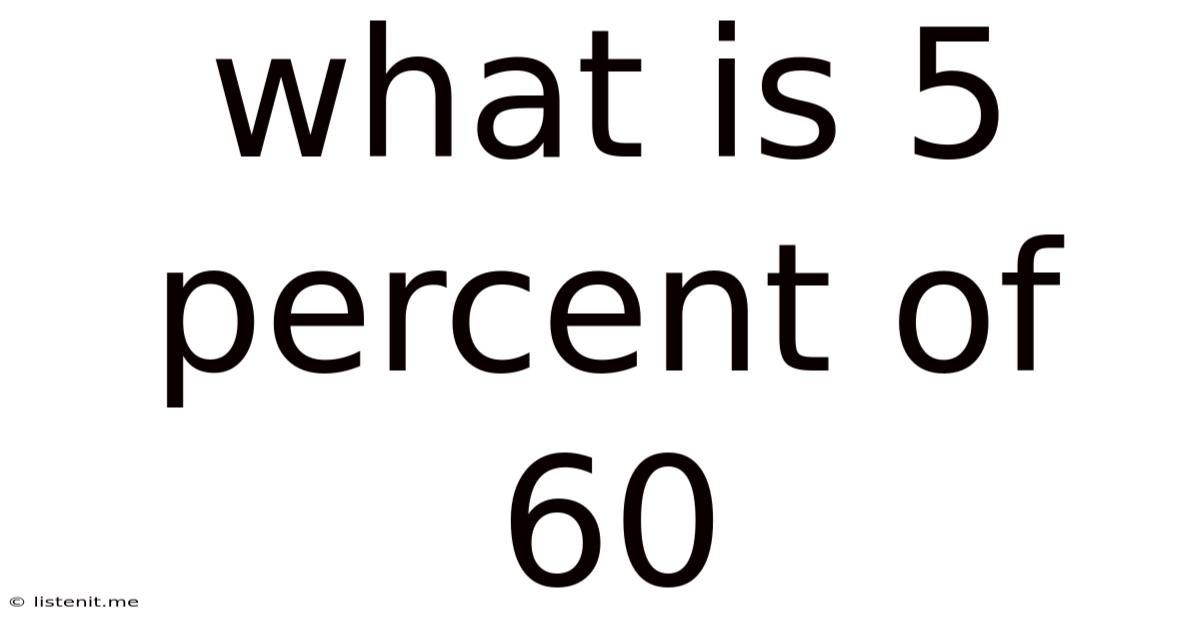
Table of Contents
What is 5 Percent of 60? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex financial analysis. This article explores the simple calculation of "What is 5 percent of 60?" and expands on the broader concept of percentages, their real-world applications, and different methods for calculating them. We will also delve into related percentage calculations and problem-solving techniques.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 5% means 5 out of 100, or 5/100. Understanding this basic definition is crucial for solving percentage problems.
The Formula for Calculating Percentages
The core formula for calculating a percentage of a number is:
(Percentage/100) * Number = Result
In our case, we want to find 5% of 60. Applying the formula:
(5/100) * 60 = 3
Therefore, 5% of 60 is 3.
Different Methods for Calculating 5% of 60
While the formula above is the most straightforward, several other methods can calculate 5% of 60. These alternative approaches offer valuable insights into percentage calculations and can be particularly helpful in different contexts.
Method 1: Using Decimal Equivalents
Percentages can be easily converted to decimal equivalents by dividing the percentage by 100. 5% as a decimal is 0.05 (5/100 = 0.05). Therefore, calculating 5% of 60 becomes:
0.05 * 60 = 3
Method 2: Using Fractions
As mentioned earlier, 5% can be expressed as the fraction 5/100. This fraction can be simplified to 1/20. Therefore:
(1/20) * 60 = 3
Method 3: Proportion Method
This method utilizes proportions to solve the problem. We set up a proportion where 'x' represents the unknown value (5% of 60):
5/100 = x/60
Cross-multiplying, we get:
100x = 300
Dividing both sides by 100:
x = 3
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in daily life. Here are some examples:
- Sales and Discounts: Stores frequently advertise discounts as percentages (e.g., "20% off"). Calculating the actual discount requires percentage calculations.
- Taxes: Sales taxes, income taxes, and other taxes are often expressed as percentages.
- Tips and Gratuities: Calculating tips in restaurants typically involves determining a percentage of the bill.
- Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages.
- Financial Analysis: Percentage changes in stock prices, profits, and other financial metrics are crucial for investment decisions.
- Statistics and Data Analysis: Percentages are essential for summarizing and interpreting data, representing proportions and probabilities.
- Scientific Research: Percentages are used to express changes or relationships in scientific experiments and observations.
Expanding on Percentage Calculations: Related Problems
Understanding the calculation of 5% of 60 lays the groundwork for tackling more complex percentage problems. Let's explore some related scenarios:
Finding the Percentage One Number Represents of Another
What percentage of 60 is 3?
To find this, we use the formula:
(Part/Whole) * 100 = Percentage
In this case, the part is 3, and the whole is 60:
(3/60) * 100 = 5%
Calculating Percentage Increase or Decrease
If a value increases from 60 to 63, what is the percentage increase?
- Find the difference: 63 - 60 = 3
- Divide the difference by the original value: 3/60 = 0.05
- Multiply by 100 to express as a percentage: 0.05 * 100 = 5%
Therefore, the percentage increase is 5%. A similar method is used for percentage decrease.
Working with Multiple Percentages
What is 10% of 60, and then 5% of that result?
- Calculate 10% of 60: (10/100) * 60 = 6
- Calculate 5% of 6: (5/100) * 6 = 0.3
Therefore, 10% of 60, and then 5% of that result is 0.3. These types of multi-step calculations are common in various applications.
Advanced Percentage Calculations and Applications
While the examples above cover basic percentage calculations, more advanced concepts exist, including:
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest.
- Exponential Growth and Decay: Percentages are used to model phenomena exhibiting exponential growth or decay, such as population growth or radioactive decay.
- Financial Modeling: Sophisticated financial models often rely heavily on percentage calculations to forecast future performance and assess risk.
Conclusion
Calculating 5% of 60, while seemingly simple, provides a foundation for understanding and applying percentage calculations across a vast range of disciplines. Mastering this skill is essential for success in numerous personal and professional contexts. By understanding the various methods and their applications, you can approach percentage problems with greater confidence and efficiency. Remember to practice regularly to build your proficiency and explore more advanced percentage applications to further enhance your skills. The ability to effortlessly work with percentages will greatly benefit you in many aspects of life.
Latest Posts
Latest Posts
-
How Many Months Is 2000 Days
May 24, 2025
-
What Is The Prime Factorization Of 175
May 24, 2025
-
7 5 8 As An Improper Fraction
May 24, 2025
-
Calories Burned Walking In Water Calculator
May 24, 2025
-
15 To The Power Of 5
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.