85 Of 27 Is What Number
listenit
May 25, 2025 · 4 min read
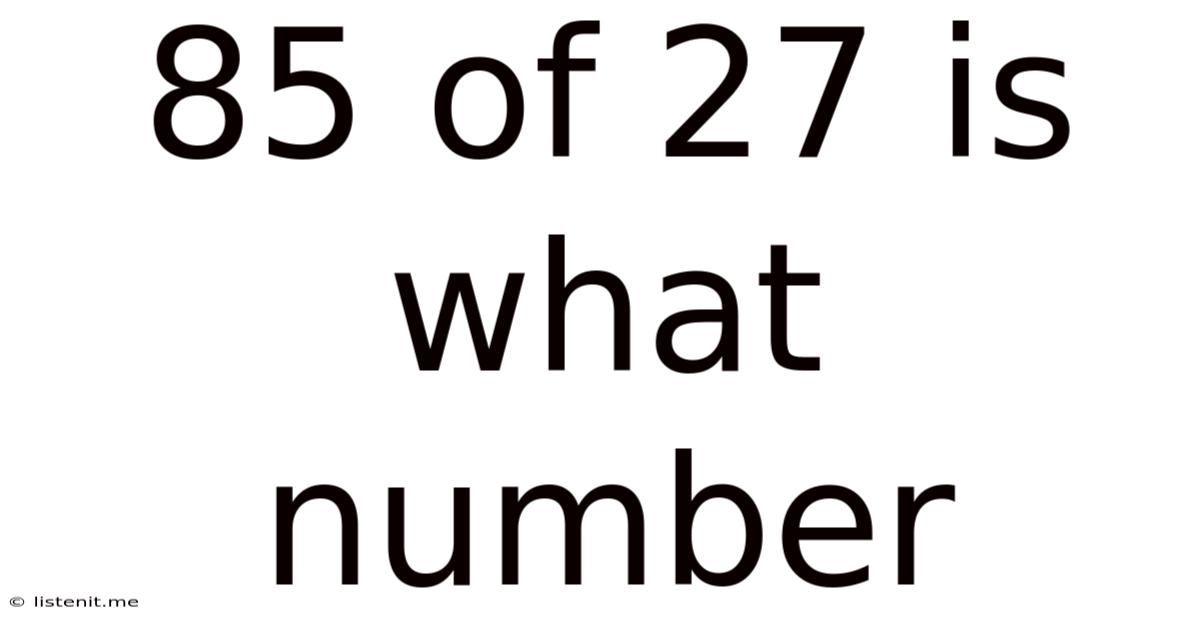
Table of Contents
Decoding Percentages: A Deep Dive into "85% of 27 is What Number?"
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex financial analysis and scientific research. This article will delve into the question, "85% of 27 is what number?", providing not only the answer but a comprehensive explanation of the underlying principles and various methods for solving percentage problems. We'll explore different approaches, focusing on clarity and practicality, ensuring you confidently tackle similar calculations in the future.
Understanding Percentages: The Basics
A percentage represents a fraction of 100. The term "percent" literally means "per hundred." Therefore, 85% means 85 out of 100, or 85/100. This fraction can be simplified to 17/20. Understanding this fundamental concept is crucial for solving percentage problems.
Method 1: Converting Percentage to Decimal
This is arguably the most straightforward method for calculating percentages. The process involves converting the percentage to its decimal equivalent and then multiplying it by the given number.
Step 1: Convert the percentage to a decimal.
To convert 85% to a decimal, divide it by 100:
85% ÷ 100 = 0.85
Step 2: Multiply the decimal by the given number.
Now, multiply the decimal (0.85) by 27:
0.85 x 27 = 22.95
Therefore, 85% of 27 is 22.95
Method 2: Using Fractions
This method utilizes the fractional representation of the percentage.
Step 1: Express the percentage as a fraction.
As mentioned earlier, 85% can be written as 85/100, which simplifies to 17/20.
Step 2: Multiply the fraction by the given number.
Multiply the fraction (17/20) by 27:
(17/20) x 27 = 459/20
Step 3: Convert the improper fraction to a decimal.
Divide the numerator (459) by the denominator (20):
459 ÷ 20 = 22.95
Therefore, 85% of 27 is 22.95
Method 3: Proportion Method
This method sets up a proportion to solve for the unknown value.
Step 1: Set up the proportion.
We can set up a proportion as follows:
85/100 = x/27
Where 'x' represents the unknown value (85% of 27).
Step 2: Cross-multiply.
Cross-multiplying gives us:
100x = 85 x 27
100x = 2295
Step 3: Solve for x.
Divide both sides by 100:
x = 2295 ÷ 100
x = 22.95
Therefore, 85% of 27 is 22.95
Applying Percentage Calculations in Real-World Scenarios
Understanding percentage calculations is crucial for navigating various real-world situations. Here are a few examples:
-
Sales and Discounts: Calculating discounts offered during sales is a prime example. If a store offers an 85% discount on a $27 item, the discount amount would be 22.95.
-
Tax Calculations: Determining the amount of sales tax or VAT added to a purchase involves percentage calculations.
-
Investment Returns: Calculating investment returns, profit margins, and interest earned often relies on percentage calculations.
-
Data Analysis: Percentages are frequently used in data analysis to represent proportions and trends. For example, analyzing survey results often requires expressing responses as percentages.
Beyond the Basics: Advanced Percentage Problems
While the problem "85% of 27" is relatively straightforward, percentage problems can become more complex. Here are some examples of more advanced problems and how to approach them:
-
Finding the percentage: Instead of finding a percentage of a number, you might need to find what percentage one number is of another. For instance, "What percentage of 27 is 20?"
-
Finding the original number: You might know the percentage and the resulting value and need to find the original number. For example, "22.95 is 85% of what number?"
Solving these more advanced problems often requires rearranging the basic percentage formula (Percentage = (Part/Whole) x 100) and applying algebraic principles.
Tips and Tricks for Mastering Percentage Calculations
-
Practice Regularly: The more you practice, the more comfortable you'll become with percentage calculations.
-
Use a Calculator: Don't hesitate to use a calculator, especially for more complex problems.
-
Check Your Work: Always double-check your calculations to ensure accuracy.
-
Understand the Context: Pay close attention to the wording of the problem to understand what is being asked.
-
Break Down Complex Problems: If a problem seems overwhelming, break it down into smaller, more manageable steps.
Conclusion: Mastering Percentages for Success
Understanding and mastering percentage calculations is a crucial skill with broad applications across various aspects of life. By understanding the fundamental principles, exploring different calculation methods, and practicing regularly, you can confidently tackle percentage problems of varying complexity. This article has provided a comprehensive guide, from basic calculations to more advanced applications, empowering you to handle percentage-related challenges with ease and precision. Remember, consistent practice is key to solidifying your understanding and building your confidence in this essential mathematical skill. The ability to quickly and accurately calculate percentages will undoubtedly enhance your problem-solving skills and provide a significant advantage in many areas of life and work.
Latest Posts
Latest Posts
-
2 Divided By What Equals 1 34
May 25, 2025
-
30 Year Mortgage On 150 000
May 25, 2025
-
How Many Hours Are In 30 Years
May 25, 2025
-
3 4 19 And 5 6 41 Than 1 3
May 25, 2025
-
What Year Was A 25 Year Old Born
May 25, 2025
Related Post
Thank you for visiting our website which covers about 85 Of 27 Is What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.