3 4 19 And 5 6 41 Than 1 3
listenit
May 25, 2025 · 5 min read
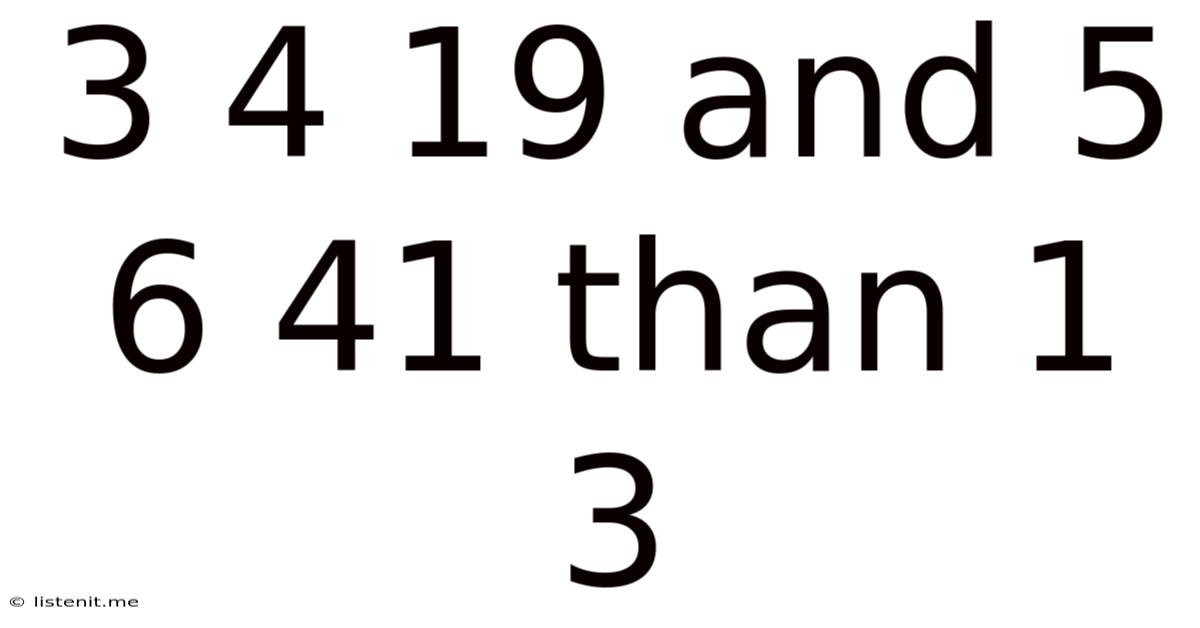
Table of Contents
Unraveling the Mystery: The Patterns and Possibilities of 3 4 19, 5 6 41, and 1 3
The seemingly innocuous number sequences "3 4 19," "5 6 41," and "1 3" might appear random at first glance. However, a deeper dive reveals a fascinating potential for mathematical patterns, logical connections, and creative interpretations. This exploration will delve into various perspectives, examining potential underlying rules, exploring mathematical functions, and considering the implications of these sequences within broader numerical contexts. We’ll also investigate how these seemingly disparate sets might be related. This analysis aims to uncover the hidden logic and demonstrate the enriching experience of deciphering numerical puzzles.
Potential Mathematical Relationships: Exploring the Patterns
The initial challenge lies in identifying a consistent relationship between the numbers within each sequence and across the sequences. Let's examine the individual sets:
1. Analyzing 3 4 19:
The most straightforward approach involves looking for simple arithmetic operations. Adding, subtracting, multiplying, and dividing the first two numbers (3 and 4) doesn't directly yield 19. Let’s explore some more complex relationships:
-
Quadratic Equations: Could a quadratic equation generate this sequence? If we assume a relationship of the form ax² + bx + c, where x represents the position of the number in the sequence (x=1 for 3, x=2 for 4), we can attempt to solve for a, b, and c. This requires more data points, making a definitive answer elusive with only three numbers.
-
Nonlinear Functions: More complex nonlinear functions could generate this sequence, but without additional data, pinpointing a specific function remains speculative.
-
Pattern Recognition: Observing that 19 is close to 34 + 7 and 44 + 3 suggests a potential iterative relationship, but this isn’t conclusive without additional examples. There might be some hidden recursive relationship we haven't discovered yet.
2. Analyzing 5 6 41:
Similar to the first sequence, simple arithmetic operations fail to link 5, 6, and 41 directly. Let's consider other possibilities:
-
Higher-Order Polynomials: Higher-order polynomials might provide a better fit than quadratic equations, but, again, more data points would be beneficial for definitive solutions.
-
Geometric Progressions: The numbers are not in a simple geometric progression (a constant ratio between consecutive terms).
-
Combinatorial Relationships: Could the numbers represent a combinatorial problem, such as permutations or combinations? Without more context, this possibility remains difficult to confirm.
3. Integrating 1 3:
The short sequence "1 3" provides even less information. While it could be the beginning of an arithmetic sequence (adding 2 each time), or a section of a larger sequence, its limited length offers few clues regarding its overall nature. Its relationship to 3 4 19 and 5 6 41 remains largely mysterious.
Connecting the Sequences: A Search for Commonality
The primary challenge now becomes establishing a link between the three sequences. Are they connected by a unified rule or are they unrelated yet share some subtle underlying principle?
-
Iterative Relationships: One could hypothetically construct an iterative process where a function takes as input the previous sequence and generates the next. However, defining this function requires a significant amount of speculation without additional sequences.
-
Modular Arithmetic: Exploring modular arithmetic (arithmetic with remainders) might reveal hidden patterns. For example, examining the remainders after division by certain numbers across the sequences could uncover unexpected links.
-
Geometric Interpretations: A more abstract approach could involve visualizing the sequences as points in a coordinate system and looking for geometric relationships between them. This could reveal patterns not immediately evident from a purely numerical perspective.
Expanding the Possibilities: Incorporating External Factors
To enhance the chances of discovering underlying rules, we need to expand the scope of the inquiry:
-
Additional Sequences: The inclusion of additional sequences similar to the initial three would significantly improve the potential for uncovering a general rule. A larger dataset would facilitate the application of more advanced mathematical techniques like regression analysis or machine learning.
-
Contextual Information: Any contextual clues surrounding the origin of these sequences could be critical in deciphering their meaning. Where did these numbers come from? What problem are they meant to solve?
-
Alternative Number Systems: Exploring the sequences using different number systems (e.g., binary, hexadecimal) might reveal hidden patterns that are obscured in the decimal system.
Creative Interpretations: Beyond Pure Mathematics
Given the limited information, it’s also valid to consider creative and speculative interpretations, acknowledging that there might not be a single definitive mathematical solution.
-
Code Breaking: Could these be parts of a code or cipher? Further investigation would involve exploring different cryptography techniques.
-
Puzzles and Games: Perhaps these sequences are part of a larger puzzle or game. The solution might require the introduction of additional elements or clues.
Conclusion: The Ongoing Search for Answers
The sequences "3 4 19," "5 6 41," and "1 3" present a compelling puzzle. While a definitive mathematical solution might require more information, exploring various mathematical and logical possibilities highlights the richness and complexity of numerical relationships. The process of attempting to decipher these sequences demonstrates how seemingly simple numbers can lead to fascinating investigations, prompting creativity and deeper mathematical thinking. This investigation encourages us to approach numerical puzzles with a blend of rigorous analytical techniques and imaginative exploration, demonstrating the boundless possibilities within the realm of numbers and patterns. The absence of a definitive solution shouldn’t discourage us; rather, it underscores the enduring appeal of mathematical mysteries and the ongoing quest for discovery. Further research, including the acquisition of additional related data points, remains crucial to resolving this intriguing enigma.
Latest Posts
Latest Posts
-
Tangent Of A Circle Formula Calculator
May 26, 2025
-
Find The Prime Factorization Of 35
May 26, 2025
-
1 In 450 As A Percentage
May 26, 2025
-
Greatest Common Factor Of 32 And 56
May 26, 2025
-
What Is The Value Of 1410 In Binary
May 26, 2025
Related Post
Thank you for visiting our website which covers about 3 4 19 And 5 6 41 Than 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.