8 Out Of 23 As A Percentage
listenit
May 24, 2025 · 5 min read
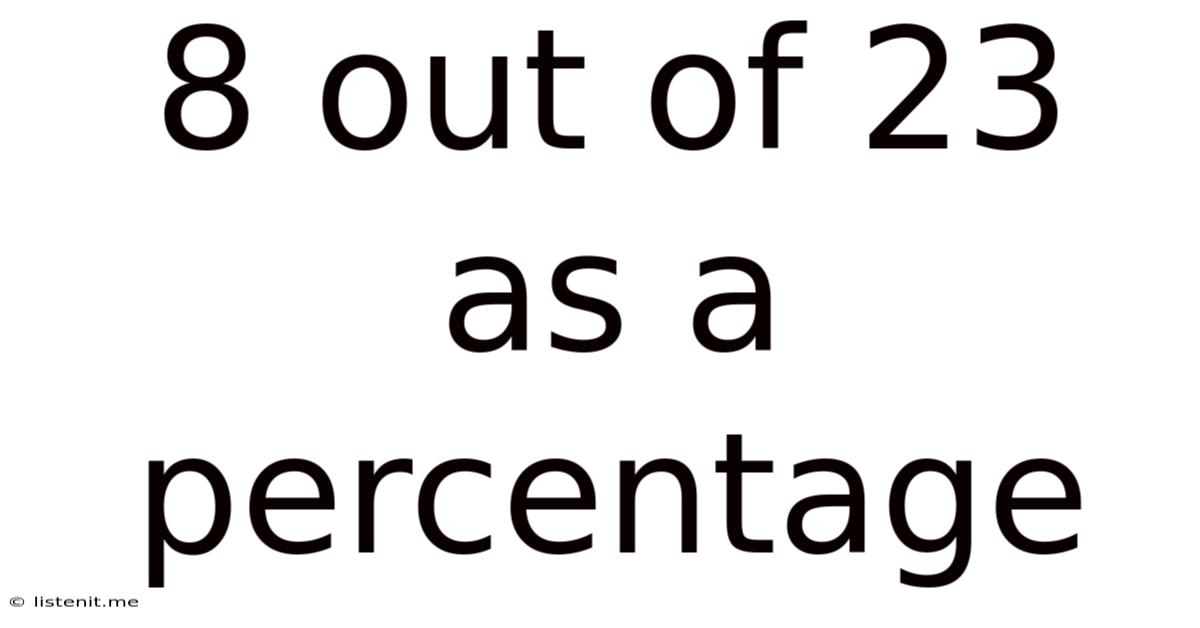
Table of Contents
8 Out of 23 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with applications across various fields, from everyday finances to complex scientific analyses. Understanding how to convert fractions and ratios into percentages is crucial for interpreting data, making informed decisions, and communicating effectively. This comprehensive guide delves into the calculation of "8 out of 23 as a percentage," explaining the process step-by-step, offering alternative methods, and exploring related percentage problems. We'll also touch on the practical applications of percentage calculations and how to improve your overall understanding.
Understanding the Basics of Percentages
Before we tackle the specific problem, let's refresh our understanding of percentages. A percentage is simply a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5.
Understanding this fundamental relationship is key to solving percentage problems. We often encounter percentages in everyday life, such as discounts in stores (e.g., "20% off"), tax rates, interest rates, and statistical data representation.
Calculating 8 Out of 23 as a Percentage: The Step-by-Step Approach
To calculate "8 out of 23" as a percentage, we need to follow these steps:
Step 1: Express the ratio as a fraction.
The phrase "8 out of 23" can be directly written as a fraction: 8/23.
Step 2: Convert the fraction to a decimal.
To convert the fraction 8/23 to a decimal, divide the numerator (8) by the denominator (23):
8 ÷ 23 ≈ 0.3478
Step 3: Convert the decimal to a percentage.
To convert the decimal 0.3478 to a percentage, multiply it by 100 and add the "%" symbol:
0.3478 × 100 ≈ 34.78%
Therefore, 8 out of 23 is approximately 34.78%.
Alternative Methods for Percentage Calculation
While the above method is straightforward, there are alternative approaches to calculating percentages, especially useful when dealing with more complex problems or when using calculators with limited functionality.
Method 1: Using Proportions
We can set up a proportion to solve for the percentage:
8/23 = x/100
Cross-multiplying, we get:
23x = 800
Solving for x:
x = 800/23 ≈ 34.78
Therefore, x ≈ 34.78%, confirming our previous result.
Method 2: Using a Calculator with Percentage Function
Most calculators have a percentage function (%) that simplifies the process. You can input 8 ÷ 23 and then press the % button. The calculator will directly display the result as a percentage.
Practical Applications of Percentage Calculations
Percentage calculations are used extensively in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns. Understanding percentages is essential for managing personal finances and making sound financial decisions.
-
Statistics: Representing data in charts and graphs, interpreting survey results, and calculating probabilities. Percentages provide a standardized way to compare and analyze data.
-
Science: Expressing concentrations of solutions, calculating experimental yields, and analyzing data in various scientific fields.
-
Retail: Determining discounts, markups, and sales tax. Retail businesses rely heavily on percentage calculations for pricing and promotions.
Understanding Percentage Increase and Decrease
Beyond basic percentage calculations, understanding percentage increase and decrease is crucial. These calculations involve determining the change in a value as a percentage of the original value.
Percentage Increase: This calculates the increase in a value as a percentage of the original value. The formula is:
[(New Value - Original Value) / Original Value] × 100%
Percentage Decrease: This calculates the decrease in a value as a percentage of the original value. The formula is:
[(Original Value - New Value) / Original Value] × 100%
Let's illustrate with an example:
Suppose the price of an item increased from $100 to $120. The percentage increase is:
[(120 - 100) / 100] × 100% = 20%
Common Mistakes to Avoid When Calculating Percentages
While percentage calculations are relatively straightforward, several common mistakes can lead to inaccurate results. Here are some crucial points to remember:
-
Order of operations: Always follow the order of operations (PEMDAS/BODMAS) when performing calculations involving multiple operations. Incorrect order can lead to significantly different results.
-
Decimal placement: Ensure accurate decimal placement when converting fractions to decimals and decimals to percentages. Even a slight error in decimal placement can affect the final percentage.
-
Rounding: Rounding off numbers too early in the calculation process can introduce significant errors. It's recommended to round only the final result to the desired level of precision.
-
Understanding the context: Always carefully consider the context of the problem. Understanding what the percentage represents in relation to the original value is critical for accurate interpretation.
Improving Your Percentage Calculation Skills
Mastering percentage calculations requires practice and a solid understanding of the underlying concepts. Here are some tips to improve your skills:
-
Practice regularly: Solve various percentage problems to build confidence and fluency. Start with simple problems and gradually increase the complexity.
-
Use different methods: Familiarize yourself with various methods for calculating percentages, such as using fractions, decimals, proportions, and calculators. This provides flexibility and allows you to choose the most efficient method for a given problem.
-
Check your work: Always double-check your calculations to ensure accuracy. Use alternative methods to verify your results.
-
Seek help when needed: Don't hesitate to seek help if you encounter difficulties. Consult textbooks, online resources, or ask a teacher or tutor for assistance.
Conclusion: Mastering Percentages for Real-World Success
Calculating percentages is a crucial life skill with broad applications. Understanding the different methods and potential pitfalls ensures accuracy and builds confidence in handling numerical problems. By mastering percentage calculations, you’ll be better equipped to tackle challenges in finance, statistics, science, and many other fields. Remember to practice regularly, understand the underlying principles, and check your work meticulously to achieve mastery in this essential skill. The seemingly simple problem of "8 out of 23 as a percentage" serves as a stepping stone to understanding the broader world of percentage calculations and their invaluable role in various aspects of life.
Latest Posts
Latest Posts
-
Find The Measure Of Side C
May 25, 2025
-
What Is 35 Percent Of 140
May 25, 2025
-
What Is 1 2 Of 24
May 25, 2025
-
Calculate Dew Point From Wet Bulb And Dry Bulb
May 25, 2025
-
Greatest Common Factor Of 175 And 25
May 25, 2025
Related Post
Thank you for visiting our website which covers about 8 Out Of 23 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.