What Is 35 Percent Of 140
listenit
May 25, 2025 · 5 min read
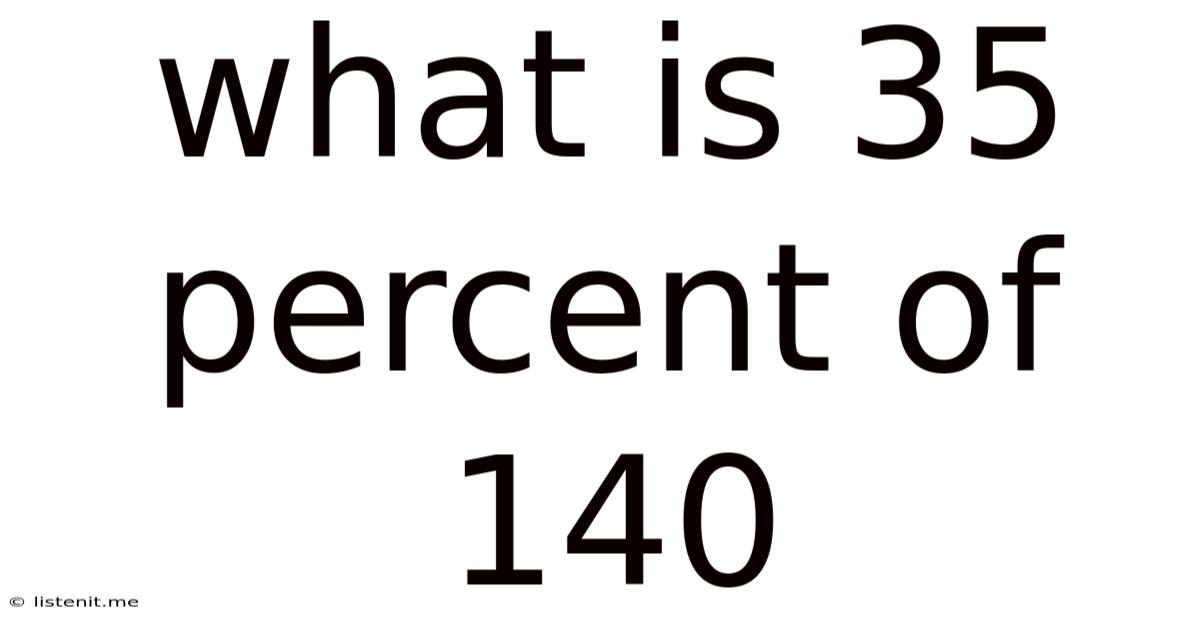
Table of Contents
What is 35 Percent of 140? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with widespread applications in various aspects of life. From understanding sales discounts and tax calculations to analyzing financial statements and comprehending statistical data, the ability to quickly and accurately determine percentages is invaluable. This article will thoroughly explore how to calculate 35% of 140, delve into the underlying principles of percentage calculations, and illustrate their practical applications across numerous fields.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred." The symbol % is used to denote percentages. For instance, 35% can be written as 35/100 or 0.35 as a decimal. This representation is crucial for performing percentage calculations.
Key Concepts:
- Percent: Represents a portion of a whole, expressed as a fraction of 100.
- Base: The original number or quantity from which the percentage is calculated (in this case, 140).
- Rate: The percentage itself (in this case, 35%).
- Portion: The result of the calculation (what we aim to find - 35% of 140).
Calculating 35% of 140: Three Methods
There are several ways to calculate 35% of 140. Let's explore three common methods:
Method 1: Using Decimal Conversion
This is arguably the most straightforward method. We convert the percentage to its decimal equivalent and then multiply it by the base number:
- Convert the percentage to a decimal: 35% = 35/100 = 0.35
- Multiply the decimal by the base number: 0.35 * 140 = 49
Therefore, 35% of 140 is 49.
Method 2: Using Fraction Conversion
This method involves converting the percentage to a fraction and then multiplying it by the base number:
- Convert the percentage to a fraction: 35% = 35/100
- Simplify the fraction (if possible): 35/100 simplifies to 7/20
- Multiply the fraction by the base number: (7/20) * 140 = 7 * 7 = 49
Again, we find that 35% of 140 is 49.
Method 3: Using Proportions
This method uses the concept of proportions to solve the problem:
We can set up a proportion:
35/100 = x/140
Where 'x' represents the unknown portion we're trying to find. To solve for x, we cross-multiply:
35 * 140 = 100 * x
4900 = 100x
x = 4900 / 100
x = 49
Thus, 35% of 140 is 49.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world scenarios. Here are some examples:
1. Sales and Discounts:
Retail stores frequently offer discounts on products, often expressed as percentages. Understanding percentage calculations allows consumers to quickly determine the actual price after a discount. For example, a 35% discount on a $140 item would result in a saving of $49, making the final price $91.
2. Taxes:
Sales tax, income tax, and other taxes are often calculated as a percentage of the base amount. Understanding percentage calculations is crucial for determining the total cost of goods and services, including taxes.
3. Finance:
Percentages are fundamental in finance. Interest rates, loan calculations, investment returns, and profit margins are all expressed and calculated using percentages. Understanding these calculations is essential for making informed financial decisions.
4. Statistics:
Percentages are extensively used in statistics to represent data and analyze trends. For instance, in survey results, data is often presented as percentages to easily understand the proportion of respondents who chose a particular option.
5. Scientific Research:
In scientific research, percentages are used to express error margins, variability, and proportions within data sets. This is crucial for interpreting experimental results and drawing meaningful conclusions.
Beyond the Basics: More Complex Percentage Problems
While calculating 35% of 140 is a relatively simple example, the principles involved can be applied to more complex percentage problems. Here are a few examples:
-
Finding the percentage increase or decrease: If a value increases from 140 to 161, the percentage increase can be calculated using the formula: [(New Value - Original Value) / Original Value] * 100%.
-
Finding the original value when a percentage is known: If a discounted price is $91 after a 35% discount, the original price can be calculated using the formula: Discounted Price / (1 - Discount Rate).
-
Calculating compound interest: Compound interest calculations involve repeatedly applying a percentage increase over time. This is a more complex application of percentage calculations, but understanding the underlying principles is crucial for managing finances effectively.
Mastering Percentages: Tips and Tricks
Here are some tips for mastering percentage calculations:
-
Practice regularly: The more you practice, the better you will become at solving percentage problems quickly and accurately.
-
Use different methods: Try different methods (decimal conversion, fraction conversion, and proportions) to find the method that works best for you.
-
Understand the underlying concepts: A solid understanding of the principles of percentages is crucial for tackling complex problems.
-
Use calculators and online tools: Calculators and online tools can be useful for more complex calculations. However, it is still important to understand the underlying principles to interpret the results correctly.
-
Break down complex problems: Break down complex problems into smaller, more manageable steps. This will make them easier to solve.
Conclusion: The Importance of Percentage Calculations in Everyday Life
As demonstrated throughout this article, the ability to calculate percentages is an essential life skill applicable to a wide range of situations. From navigating everyday purchases and managing finances to interpreting statistical data and understanding scientific concepts, a firm grasp of percentage calculations is indispensable for making informed decisions and thriving in today's world. The simple calculation of 35% of 140 serves as a foundation upon which a deeper understanding of percentages and their multifaceted applications can be built. By mastering this fundamental skill, you equip yourself with a valuable tool for navigating the complexities of modern life.
Latest Posts
Latest Posts
-
Find The Greatest Common Factor Of 15 And 42
May 25, 2025
-
What Is The Gcf Of 3 And 12
May 25, 2025
-
8 Out Of 14 Is What Percent
May 25, 2025
-
1979 To 2023 How Many Years
May 25, 2025
-
Find The Quotient Of The Following
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 35 Percent Of 140 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.