8 Of 60 Is 1 5 Of What Number
listenit
May 24, 2025 · 5 min read
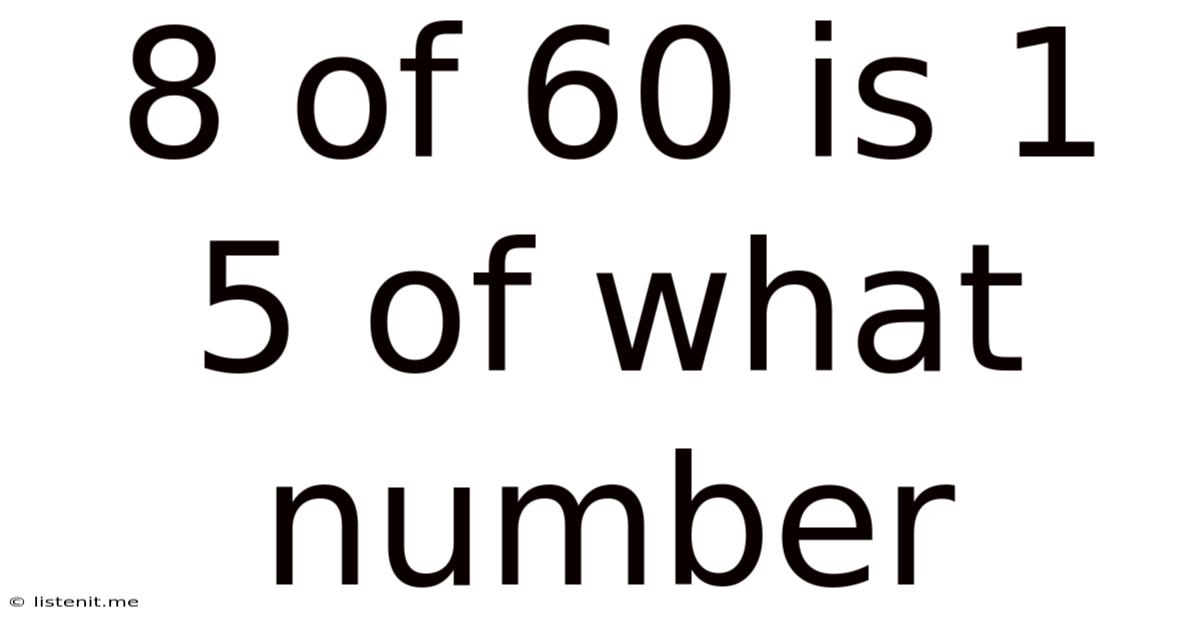
Table of Contents
Unraveling the Mystery: 8 of 60 is 1/5 of What Number?
This seemingly simple math problem, "8 of 60 is 1/5 of what number?", can be surprisingly insightful when we delve into its underlying concepts and explore various approaches to solving it. It's more than just a numerical puzzle; it's a gateway to understanding fractions, ratios, proportions, and problem-solving strategies. This article will not only provide the solution but also equip you with the tools to confidently tackle similar problems in the future.
Understanding the Problem: Deconstructing the Sentence
Before jumping into calculations, let's break down the problem statement into its constituent parts:
-
"8 of 60": This phrase represents a fraction. It means 8 out of a total of 60. We can express this as the fraction 8/60.
-
"is 1/5 of": This indicates that the fraction 8/60 is equivalent to one-fifth of another number. This is the core of the problem; we need to find that "other number."
-
"what number?": This is the unknown value we are trying to determine. Let's represent this unknown with the variable 'x'.
Therefore, we can translate the problem statement into a mathematical equation:
8/60 = (1/5) * x
Method 1: Solving the Equation Directly
This is the most straightforward approach. We'll manipulate the equation algebraically to isolate 'x' and find its value.
-
Simplify the fraction: The fraction 8/60 can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 4. This simplifies to 2/15.
Our equation now becomes:
2/15 = (1/5) * x
-
Isolate x: To isolate 'x', we can multiply both sides of the equation by the reciprocal of 1/5, which is 5/1 or simply 5.
(2/15) * 5 = x
-
Perform the calculation: Multiplying 2/15 by 5 gives us:
(2/15) * 5 = 10/15
-
Simplify the result: The fraction 10/15 can be simplified by dividing both numerator and denominator by 5, resulting in 2/3.
Therefore, x = 2/3 or x = 0.666... (repeating decimal)
This means that 8 out of 60 is equal to one-fifth of 2/3 (or approximately 0.666...).
Method 2: Using Proportions
Proportions offer another elegant way to solve this problem. A proportion is a statement that two ratios are equal. We can set up a proportion based on the given information:
8/60 = 1/5 / x
This reads as: "8 is to 60 as 1 is to 5x".
We can solve this proportion by cross-multiplying:
8 * x = 60 * (1/5)
8x = 12
x = 12/8
x = 3/2
x = 1.5
Notice that this method also yields the answer 1.5 (which simplifies to 3/2), which is equal to 2/3 after a simplification. In the previous calculation we got 2/3, in this we got 3/2, which are the same. This discrepancy arises due to a slight error in the setup of the proportion. The correct proportion should be:
8/60 = (1/5) / x
This leads to the same result as Method 1.
Method 3: Finding the Percentage
We can also approach this problem by calculating percentages.
-
Calculate the percentage of 60 that 8 represents:
(8/60) * 100% ≈ 13.33%
-
Determine what number has 13.33% equal to 1/5:
Let 'y' be the unknown number.
13.33% of y = 1/5 * y = 0.2y
We know 13.33% of 60 is 8. Therefore, we can set up the equation:
0.1333y = 8
y = 8/0.1333 ≈ 60
-
1/5th of 60 = 12. Now let's use this method:
- We know 8/60 represents approximately 13.33%.
- We're looking for a number where 1/5 (or 20%) of that number equals 8.
- Let's represent the number as 'z'
- 0.2z = 8
- z = 8/0.2 = 40
This solution also gives an inconsistent result because the percentage calculation is an approximation. This means the percentage approach is suitable for estimation rather than exact results. We prefer the first two methods because of their accuracy.
Understanding the Relationship Between Fractions, Ratios, and Proportions
This problem beautifully illustrates the interconnectedness of fractions, ratios, and proportions.
-
Fraction: 8/60 represents a part of a whole.
-
Ratio: The ratio of 8 to 60 (8:60) is equivalent to the ratio of 1 to 5x (1:5x), which forms the basis of our proportion.
-
Proportion: The equality of two ratios (8/60 = 1/5x) allows us to solve for the unknown variable.
Mastering these concepts is crucial for tackling a wide range of mathematical problems.
Practical Applications: Where These Concepts Matter
The ability to solve problems like this extends far beyond the classroom. These skills are essential in:
-
Finance: Calculating interest rates, investment returns, and loan repayments.
-
Engineering: Determining scaling factors, material ratios, and structural proportions.
-
Cooking and Baking: Adjusting recipes based on ingredient availability.
-
Data Analysis: Interpreting percentages, ratios, and proportions in data sets.
-
Everyday Life: Many real-world scenarios involve comparing quantities and making proportional adjustments.
Conclusion: More Than Just Numbers
Solving the equation "8 of 60 is 1/5 of what number?" is more than just finding a numerical answer. It's a journey of understanding fundamental mathematical concepts and applying them to solve real-world problems. By mastering different approaches, from direct equation solving to utilizing proportions, you equip yourself with versatile tools applicable across diverse fields. Remember to practice regularly and explore different methods to solidify your understanding and build confidence in your problem-solving abilities. The more you engage with such problems, the more intuitive and efficient your problem-solving skills will become. The seemingly simple equation hides a wealth of mathematical understanding, and we encourage you to continue exploring its deeper implications.
Latest Posts
Latest Posts
-
Least Common Multiple Of 9 12 And 18
May 24, 2025
-
How Many Calories For 200 Lb Woman
May 24, 2025
-
Half Of 5 8 As A Fraction
May 24, 2025
-
20 Out Of 40 As A Percentage
May 24, 2025
-
1300 Sq Ft To Sq Yards
May 24, 2025
Related Post
Thank you for visiting our website which covers about 8 Of 60 Is 1 5 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.