8 8 4 X 3 Solution
listenit
May 26, 2025 · 5 min read
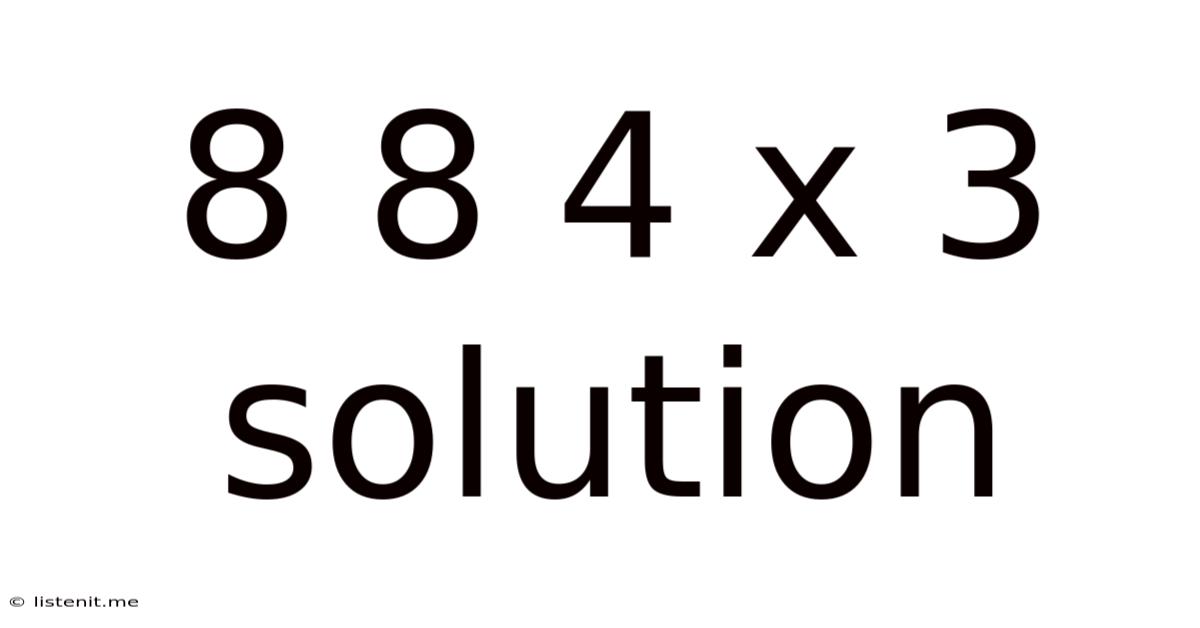
Table of Contents
Decoding the Enigma: Exploring Solutions to 8 8 4 x 3
The seemingly simple equation, "8 8 4 x 3," presents a fascinating challenge, particularly when interpreted as a mathematical puzzle rather than a straightforward multiplication problem. This ambiguity allows for multiple interpretations and solutions, engaging the mind and fostering critical thinking. This article delves deep into the various approaches to solving this puzzle, exploring different mathematical operations and showcasing the creative thinking required to find multiple answers. We'll examine the problem from multiple perspectives, from the basic arithmetic interpretation to more complex scenarios that involve incorporating order of operations and unconventional mathematical concepts.
The Obvious Approach: Standard Multiplication
The most straightforward interpretation treats this as a simple multiplication problem. In this case, we'd perform the operations in the order they appear:
- Concatenation: Combine the numbers 8, 8, and 4 to form the number 884.
- Multiplication: Multiply 884 by 3.
This leads us to the solution: 884 x 3 = 2652. This is a valid and straightforward solution, but it doesn't explore the full potential of the problem's ambiguity. The puzzle's beauty lies in its openness to more creative interpretations.
Beyond the Basics: Exploring Alternative Interpretations
The lack of explicit operators between the numbers allows for a degree of freedom. We can explore alternative interpretations using different mathematical operations, leading to significantly different results. Let's consider some variations:
Utilizing Addition and Multiplication
One possible approach involves incorporating addition alongside multiplication. This opens up a range of possibilities:
- Grouping and Multiplication: We could group the numbers in different ways, for example: (8 + 8 + 4) x 3 = 20 x 3 = 60.
- Sequential Operations: Another option is to perform operations sequentially: (8 x 8) + 4 x 3 = 64 + 12 = 76.
- Combined Operations: A more complex solution could involve a combination of addition and multiplication: (8 + 8) x (4 + 3) = 16 x 7 = 112.
These examples illustrate how simple changes in the order of operations and the inclusion of addition significantly alter the final result. This highlights the importance of considering all possible interpretations when tackling mathematical puzzles.
Introducing Subtraction and Division
Expanding the operational toolkit to include subtraction and division significantly increases the number of potential solutions. Consider these possibilities:
- Subtraction and Multiplication: (8 – 8) + 4 x 3 = 0 + 12 = 12. This demonstrates how subtraction can drastically simplify the equation.
- Division and Multiplication: (8 / 8) x 4 x 3 = 1 x 4 x 3 = 12. Similarly, division can dramatically change the result.
- Combined Operations (Subtraction & Division): (8 + 8 - 4) / 3 = 4 This demonstrates that incorporating subtraction and division can yield single-digit solutions as well.
The inclusion of these operations adds layers of complexity and necessitates a thorough examination of different combinations to arrive at all possible solutions.
Advanced Techniques: Exploring Factorials and Exponents
To further expand the scope of potential solutions, let's consider more advanced mathematical concepts:
Introducing Factorials
Factorials (represented by the "!" symbol) add another layer of complexity. Let's see how factorials influence the potential outcomes:
- Partial Factorial: 8! + 8 + 4 x 3. This would involve calculating 8! (8 x 7 x 6 x 5 x 4 x 3 x 2 x 1) and then proceeding with addition and multiplication. The result would be a much larger number. (Note: The specific calculation is omitted here to maintain brevity, but it could be a valid calculation depending on the imposed order of operations).
This illustrates how seemingly simple additions of mathematical concepts can generate dramatically different solutions.
Incorporating Exponents
Exponents significantly increase the magnitude of the final result. Consider these examples:
- Base 8 Exponents: 8^2 + 8 + 4 x 3. This involves squaring the number 8 (8 x 8) before performing the remaining operations.
- Base 8 and 3 Exponents: 8^3 + 4 x 3. This employs a higher exponent of 8, which would significantly impact the outcome.
The use of exponents introduces a significant challenge in finding all solutions, particularly when considering various combinations and orders of operation.
The Importance of Order of Operations (PEMDAS/BODMAS)
The order of operations (PEMDAS/BODMAS) plays a crucial role in obtaining consistent results. Understanding this principle is paramount when working with equations involving multiple operations. Remember:
- Parentheses (Brackets)
- Exponents (Orders)
- Multiplication and Division (from left to right)
- Addition and Subtraction (from left to right)
By consistently applying PEMDAS/BODMAS, we can ensure that solutions are unambiguous and easily reproducible. However, the inherent ambiguity of the problem statement "8 8 4 x 3" allows for variations in interpreting the precedence of operations, which contribute to the existence of multiple solutions.
The Value of Ambiguity in Problem-Solving
The ambiguity inherent in the "8 8 4 x 3" problem is not a flaw; it's a feature. This lack of strict constraints encourages creative thinking and the exploration of different mathematical strategies. It demonstrates the importance of:
- Critical Thinking: The problem forces us to analyze the problem from multiple angles, considering different interpretations and operational approaches.
- Problem-Solving Skills: It encourages us to think outside the box and experiment with diverse mathematical techniques to discover a range of solutions.
- Mathematical Flexibility: It underscores the importance of understanding not just individual mathematical operations but also their interplay and the impact of order of operations.
By embracing the ambiguity, we can engage in a richer and more rewarding problem-solving experience.
Conclusion: Beyond a Single Answer
The puzzle "8 8 4 x 3" is a testament to the power of ambiguity in mathematical problem-solving. The seemingly simple equation unravels into a complex tapestry of potential solutions, showcasing the versatility of mathematical operations and the importance of critical and creative thinking. While the straightforward multiplication yields 2652, the numerous alternative interpretations demonstrate the value of exploring unconventional approaches and considering all possible scenarios. The exploration of different methods, from basic addition and multiplication to more advanced techniques involving factorials and exponents, reveals a richness that extends far beyond a single definitive answer. Ultimately, the puzzle’s true value lies not in finding the solution, but in the process of discovering many solutions and appreciating the flexibility and versatility of mathematics. The more we explore, the more deeply we appreciate the inherent richness and beauty of mathematics.
Latest Posts
Latest Posts
-
Most Commonly Injured Nerve In Open Inguinal Hernia Repair
May 27, 2025
-
Conceptual Adaptation Using Knowledge Graph And Semantics Ai
May 27, 2025
-
How Many Anastomosis In A Whipplel
May 27, 2025
-
Paced Auditory Serial Addition Task A Measure Of Recovery From Concussion
May 27, 2025
-
How Long Can You Live With Pleural Effusion
May 27, 2025
Related Post
Thank you for visiting our website which covers about 8 8 4 X 3 Solution . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.