7/12 Divided By 2/9 As A Fraction
listenit
May 10, 2025 · 4 min read
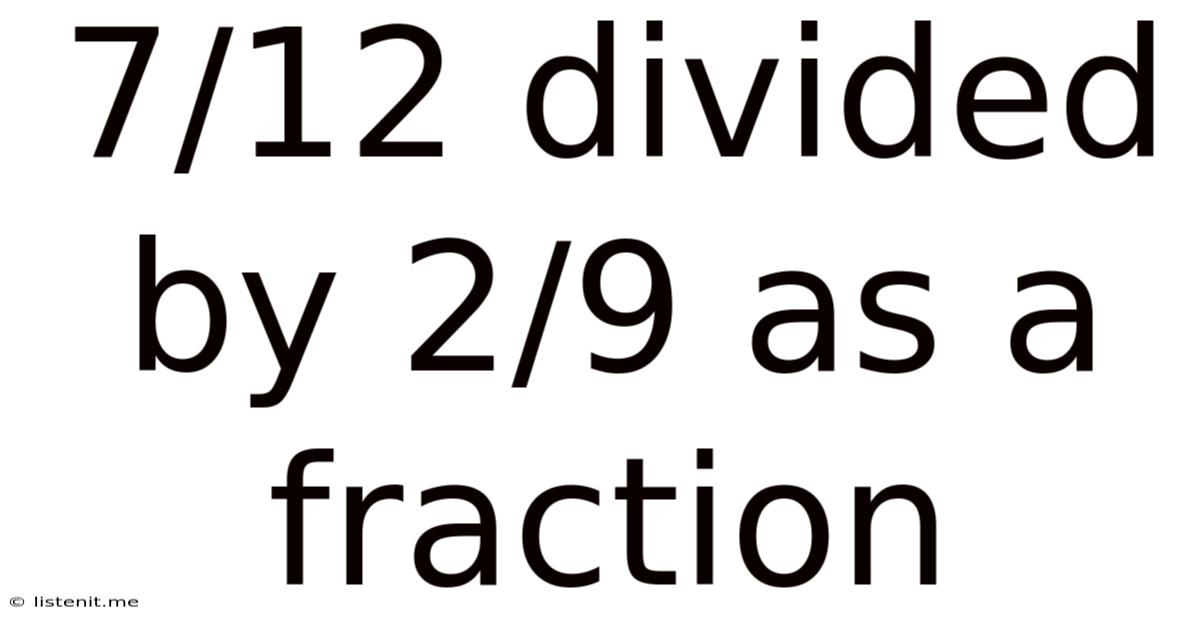
Table of Contents
7/12 Divided by 2/9 as a Fraction: A Comprehensive Guide
Dividing fractions can seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through dividing 7/12 by 2/9, explaining the steps involved and offering helpful tips and tricks to master fraction division. We'll delve into the underlying concepts, providing a solid foundation for tackling similar problems with confidence.
Understanding Fraction Division
Before we tackle the specific problem of 7/12 divided by 2/9, let's review the fundamental principles of fraction division. The core concept is to invert the second fraction (the divisor) and then multiply. This is often summarized as "keep, change, flip."
- Keep: Keep the first fraction as it is.
- Change: Change the division sign to a multiplication sign.
- Flip: Flip (or invert) the second fraction; swap the numerator and denominator.
This method transforms a division problem into a multiplication problem, which is generally easier to solve.
Step-by-Step Solution: 7/12 ÷ 2/9
Now, let's apply this method to solve 7/12 divided by 2/9:
-
Keep: We keep the first fraction, 7/12, unchanged.
-
Change: We change the division sign (÷) to a multiplication sign (×).
-
Flip: We flip the second fraction, 2/9, to become 9/2.
This transforms our problem into: 7/12 × 9/2
-
Multiply the numerators: Multiply the numerators together: 7 × 9 = 63
-
Multiply the denominators: Multiply the denominators together: 12 × 2 = 24
This gives us the resulting fraction: 63/24
- Simplify the Fraction: The fraction 63/24 can be simplified by finding the greatest common divisor (GCD) of 63 and 24. The GCD of 63 and 24 is 3. We divide both the numerator and the denominator by 3:
63 ÷ 3 = 21 24 ÷ 3 = 8
Therefore, the simplified fraction is 21/8.
- Convert to a Mixed Number (Optional): While 21/8 is a perfectly acceptable answer, it can also be expressed as a mixed number. To do this, we divide the numerator (21) by the denominator (8):
21 ÷ 8 = 2 with a remainder of 5
This means that 21/8 is equivalent to 2 5/8.
Alternative Approach: Finding the Reciprocal
Another way to approach fraction division is by understanding the concept of a reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/9 is 9/2. Dividing by a fraction is the same as multiplying by its reciprocal.
Therefore, 7/12 ÷ 2/9 can be rewritten as: 7/12 × 9/2
This leads us back to the same multiplication problem we solved earlier, resulting in the same simplified fraction of 21/8 or 2 5/8.
Practical Applications of Fraction Division
Understanding fraction division isn't just an academic exercise; it has numerous practical applications in everyday life and various fields:
-
Cooking and Baking: Scaling recipes up or down requires dividing fractions. If a recipe calls for 1/2 cup of flour, and you want to make half the recipe, you'll need to divide 1/2 by 2.
-
Sewing and Crafting: Calculating fabric or yarn requirements often involves dividing fractions to account for pattern pieces or desired lengths.
-
Construction and Engineering: Precise measurements in construction and engineering frequently involve fractions, and calculations often require dividing fractions to determine appropriate dimensions or quantities.
-
Finance and Budgeting: Dividing fractions can be crucial for calculating proportions of budgets or investments.
Troubleshooting Common Mistakes
When working with fraction division, several common errors can occur:
-
Forgetting to invert the second fraction: This is a frequent mistake. Always remember to flip the second fraction before multiplying.
-
Incorrectly multiplying numerators and denominators: Pay close attention when multiplying the numerators and denominators to avoid calculation errors.
-
Failing to simplify the resulting fraction: Always simplify your answer to its lowest terms by finding the greatest common divisor of the numerator and denominator.
Further Practice and Resources
To solidify your understanding of fraction division, consider practicing with similar problems. Try dividing other fractions, gradually increasing the complexity. Online resources and educational websites offer numerous practice problems and tutorials to enhance your skills.
Conclusion: Mastering Fraction Division
Dividing fractions may appear challenging initially, but by understanding the "keep, change, flip" method or the concept of reciprocals, and by practicing regularly, you can confidently tackle any fraction division problem. This detailed guide has provided a comprehensive walkthrough of solving 7/12 divided by 2/9, demonstrating the steps involved and highlighting common pitfalls to avoid. Remember to always simplify your final answer and consider converting to a mixed number if appropriate, depending on the context of the problem. With consistent practice and a solid grasp of the fundamental principles, you'll master fraction division and apply it effectively in various real-world scenarios.
Latest Posts
Latest Posts
-
Which Organelle Is Responsible For The Production Of Proteins
May 10, 2025
-
Perform The Indicated Operation 2 2
May 10, 2025
-
Energy Needed To Start A Reaction
May 10, 2025
-
Color Of The Stars From Hottest To Coldest
May 10, 2025
-
Which Is The Graph Of 4x 3y 12
May 10, 2025
Related Post
Thank you for visiting our website which covers about 7/12 Divided By 2/9 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.