Which Is The Graph Of 4x 3y 12
listenit
May 10, 2025 · 5 min read
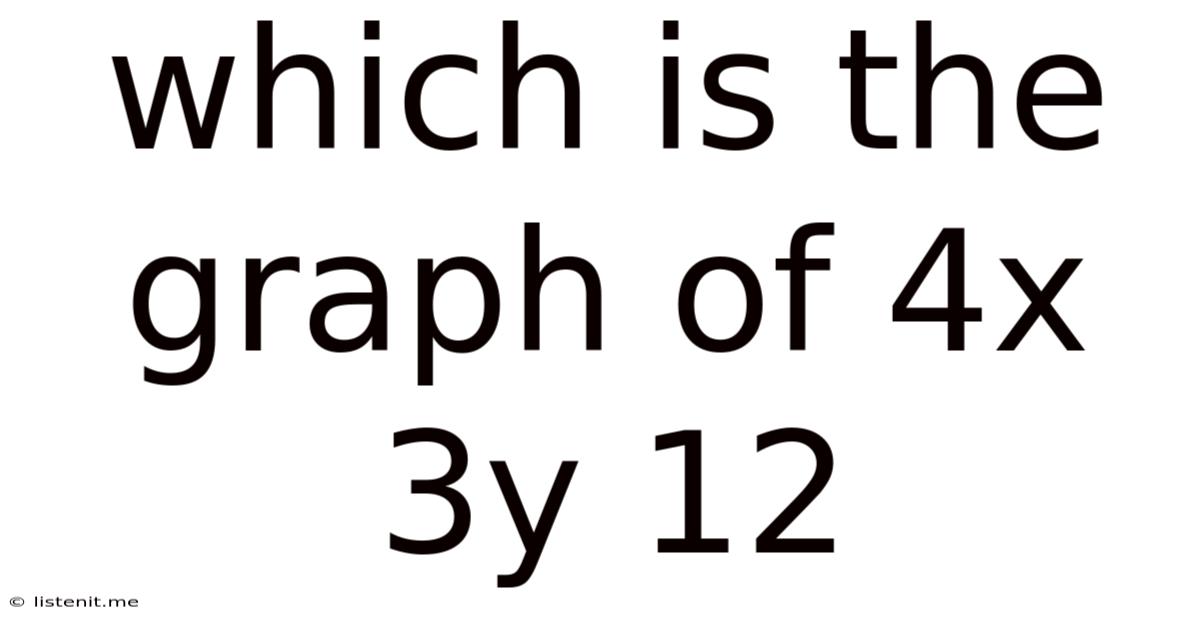
Table of Contents
Which is the Graph of 4x + 3y = 12? A Comprehensive Guide
The equation 4x + 3y = 12 represents a straight line on a Cartesian coordinate system. Understanding how to graph this line involves several key concepts in algebra and geometry. This comprehensive guide will walk you through the process step-by-step, exploring different methods, and providing insights into interpreting the results. We'll also delve into related concepts like intercepts, slope, and how to represent the line in different forms.
Understanding Linear Equations
Before we dive into graphing 4x + 3y = 12, let's refresh our understanding of linear equations. A linear equation is an equation that, when graphed, produces a straight line. It's typically written in the form:
Ax + By = C
where A, B, and C are constants, and x and y are variables. Our equation, 4x + 3y = 12, perfectly fits this mold.
Method 1: Finding the x and y-Intercepts
One of the easiest ways to graph a linear equation is by finding its x and y-intercepts.
Finding the x-intercept
The x-intercept is the point where the line crosses the x-axis. At this point, the y-coordinate is always 0. To find the x-intercept, we substitute y = 0 into the equation and solve for x:
4x + 3(0) = 12 4x = 12 x = 3
Therefore, the x-intercept is (3, 0).
Finding the y-intercept
The y-intercept is the point where the line crosses the y-axis. At this point, the x-coordinate is always 0. To find the y-intercept, we substitute x = 0 into the equation and solve for y:
4(0) + 3y = 12 3y = 12 y = 4
Therefore, the y-intercept is (0, 4).
Plotting the Intercepts and Drawing the Line
Now that we have two points, (3, 0) and (0, 4), we can plot them on a Cartesian coordinate system. Once plotted, draw a straight line connecting these two points. This line represents the graph of 4x + 3y = 12.
Method 2: Using the Slope-Intercept Form
Another common method involves converting the equation into slope-intercept form, which is:
y = mx + b
where 'm' is the slope and 'b' is the y-intercept.
Converting to Slope-Intercept Form
To convert 4x + 3y = 12 into slope-intercept form, we need to solve for y:
4x + 3y = 12 3y = -4x + 12 y = (-4/3)x + 4
Now we can clearly see that the slope (m) is -4/3 and the y-intercept (b) is 4.
Using the Slope and y-Intercept to Graph
We already know the y-intercept is (0, 4). The slope, -4/3, tells us that for every 3 units we move to the right along the x-axis, we move 4 units down along the y-axis. Starting from the y-intercept (0, 4), we can use the slope to find another point on the line. Moving 3 units to the right and 4 units down brings us to the point (3, 0), which is our x-intercept – confirming our previous calculations. Plot these two points and draw a line connecting them.
Method 3: Using Two Arbitrary Points
While the intercept method is often the easiest, you can also find any two points that satisfy the equation and use them to plot the line. Let's choose x = 1 and x = 6 as examples:
Finding the corresponding y values:
If x = 1: 4(1) + 3y = 12 3y = 8 y = 8/3
So, one point is (1, 8/3).
If x = 6: 4(6) + 3y = 12 24 + 3y = 12 3y = -12 y = -4
So, another point is (6, -4).
Plot these two points (1, 8/3) and (6, -4) and draw a line connecting them. You will find that this line is identical to the line obtained using the previous methods. This demonstrates that any two points satisfying the equation will produce the same line.
Understanding the Slope and Intercepts
The slope (-4/3) indicates the steepness and direction of the line. A negative slope signifies that the line is decreasing from left to right. The y-intercept (4) shows where the line intersects the y-axis. The x-intercept (3) shows where the line intersects the x-axis. These components provide a complete description of the line's position and orientation on the coordinate plane.
Different Forms of Linear Equations
The equation 4x + 3y = 12 is in standard form. However, linear equations can also be expressed in other forms:
- Slope-intercept form (y = mx + b): As we've seen, this form highlights the slope and y-intercept.
- Point-slope form (y - y1 = m(x - x1)): This form uses a point (x1, y1) on the line and the slope (m).
- Two-point form ((y - y1)/(x - x1) = (y2 - y1)/(x2 - x1)): This form uses two points (x1, y1) and (x2, y2) on the line.
Each form offers a unique perspective on the line's properties. Choosing the appropriate form depends on the available information and the desired focus.
Applications of Linear Equations
Linear equations are fundamental in many fields, including:
- Physics: Describing motion, relationships between variables like velocity and time.
- Economics: Modeling supply and demand, calculating costs and profits.
- Engineering: Designing structures, analyzing circuits.
- Computer science: Creating algorithms, representing data.
Understanding how to graph and manipulate linear equations is a crucial skill in these and many other disciplines.
Solving Systems of Equations involving 4x + 3y = 12
The equation 4x + 3y = 12 can be part of a system of equations. Solving a system of equations means finding the values of x and y that satisfy all the equations simultaneously. This can be done through methods like substitution, elimination, or graphical methods. Graphically, the solution would be the point where the lines intersect.
Conclusion
Graphing the equation 4x + 3y = 12 is a straightforward process, achievable through various methods. Understanding the different approaches, the significance of the slope and intercepts, and the versatility of linear equations in different forms provides a solid foundation for tackling more complex mathematical problems and real-world applications. By mastering these concepts, you'll enhance your problem-solving skills and broaden your understanding of fundamental mathematical principles. Remember to practice using different methods to solidify your understanding and build confidence in your abilities.
Latest Posts
Latest Posts
-
What Is The Largest Reservoir Of Nitrogen On Earth
May 10, 2025
-
Multicellular Organisms Can Be Organized Into What Levels
May 10, 2025
-
How Many Different Combinations Of 6 Numbers
May 10, 2025
-
How Many Molecules Of Nadh Are Produced During Glycolysis
May 10, 2025
-
Find The Value Of X Rounded To The Nearest Tenth
May 10, 2025
Related Post
Thank you for visiting our website which covers about Which Is The Graph Of 4x 3y 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.