6 Divided By What Equals 2
listenit
May 25, 2025 · 4 min read
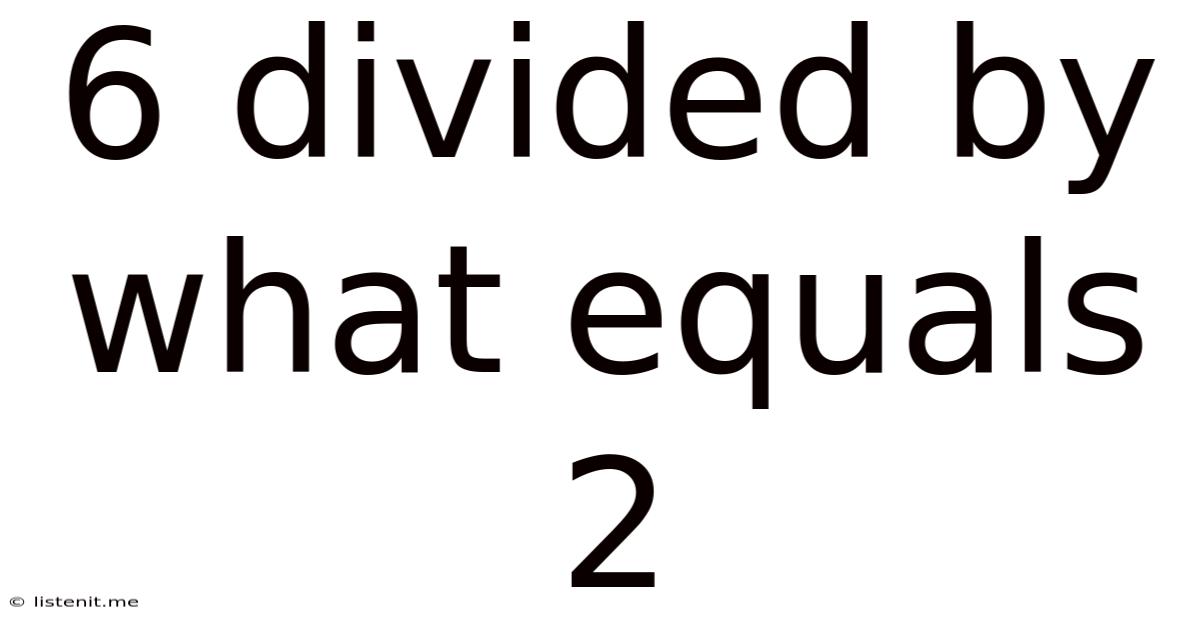
Table of Contents
6 Divided by What Equals 2? Unpacking Division and Finding the Solution
This seemingly simple question, "6 divided by what equals 2?", opens the door to a deeper understanding of division, its properties, and its applications in various mathematical contexts. While the immediate answer might seem obvious to some, exploring the problem further reveals valuable insights into fundamental mathematical concepts and problem-solving strategies. This article will not only answer the question directly but will also delve into the underlying principles, offer alternative approaches to solving similar problems, and explore the broader implications of division in mathematics and beyond.
Understanding Division: The Basics
Before diving into the specific problem, let's refresh our understanding of division. Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially represents the process of splitting a quantity into equal parts. In the expression a ÷ b = c, 'a' is the dividend (the number being divided), 'b' is the divisor (the number we're dividing by), and 'c' is the quotient (the result).
The question "6 divided by what equals 2?" can be represented algebraically as:
6 ÷ x = 2
Where 'x' is the unknown divisor we need to find.
Solving for the Unknown Divisor: Method 1 – Inverse Operation
The most straightforward method to solve this equation involves using the inverse operation of division, which is multiplication. To isolate 'x', we can multiply both sides of the equation by 'x':
6 = 2x
Now, to solve for 'x', we divide both sides by 2:
x = 6 ÷ 2
Therefore,
x = 3
This confirms that 6 divided by 3 equals 2.
Solving for the Unknown Divisor: Method 2 – Fraction Representation
Another way to approach this problem is to represent the division as a fraction:
6/x = 2
To solve for 'x', we can cross-multiply:
6 = 2x
This leads us back to the same equation as before, resulting in the same solution:
x = 3
Expanding the Concept: Different Perspectives on Division
While the solution is simple, let's examine the concept from several angles to build a more robust understanding.
Division as Repeated Subtraction
Division can be visualized as repeated subtraction. How many times can we subtract 2 from 6 before reaching 0?
6 - 2 = 4 4 - 2 = 2 2 - 2 = 0
We subtracted 2 three times, reinforcing that 6 divided by 2 equals 3. This perspective is particularly helpful for understanding division conceptually, especially for younger learners.
Division as Sharing
Imagine you have 6 cookies, and you want to share them equally among some friends such that each friend receives 2 cookies. How many friends can you share with? This scenario naturally leads to the division problem: 6 ÷ 2 = 3. This approach emphasizes the real-world application of division.
Division and Ratio
Division can also be understood as a ratio. The equation 6 ÷ x = 2 can be interpreted as the ratio of 6 to x being equal to 2 to 1. This means that for every 2 units, there are x units. This perspective is useful in various applications, such as scaling, proportions, and rates.
Applications of Division in Real-World Scenarios
Division is fundamental to countless real-world applications. Here are a few examples:
- Sharing Resources: Dividing resources equally among a group of people (e.g., splitting the bill at a restaurant).
- Calculating Averages: Finding the average of a set of numbers.
- Determining Rates: Calculating speed (distance divided by time), unit costs (total cost divided by quantity), and other rates.
- Scaling Recipes: Adjusting recipe quantities up or down.
- Financial Calculations: Calculating percentages, interest rates, and profit margins.
- Geometry: Calculating area, volume, and other geometric properties.
Extending the Problem: More Complex Division Scenarios
Let's explore a more challenging problem to further solidify our understanding of division:
"What number, when divided by 5, results in a quotient of 12 and a remainder of 3?"
This problem requires a slightly different approach. We can represent it algebraically as:
x ÷ 5 = 12 with a remainder of 3
To solve this, we first consider the quotient (12) and the divisor (5). We multiply these to find the portion of 'x' that is evenly divisible by 5:
12 × 5 = 60
Then, we add the remainder (3) to find the value of 'x':
x = 60 + 3
Therefore,
x = 63
This demonstrates that 63 divided by 5 gives a quotient of 12 and a remainder of 3.
Conclusion: The Importance of Understanding Division
The seemingly simple question, "6 divided by what equals 2?", serves as a springboard to explore the fundamental principles of division, its various interpretations, and its extensive applications. Understanding division is crucial not only for solving mathematical problems but also for navigating numerous real-world scenarios. By mastering this foundational arithmetic operation, you gain a valuable tool for problem-solving, critical thinking, and a deeper appreciation for the interconnectedness of mathematical concepts. From simple sharing of cookies to complex engineering calculations, division underpins countless processes, highlighting its vital role in our daily lives and the broader scientific world. The ability to approach problems from different perspectives – using inverse operations, fractional representations, repeated subtraction, and ratio concepts – allows for a more flexible and versatile problem-solving approach, ensuring success in tackling a wide range of mathematical challenges.
Latest Posts
Latest Posts
-
What Year Were You Born If Your 19 In 2024
May 25, 2025
-
Born In 1989 How Old Are You
May 25, 2025
-
Born In 1962 How Old Am I
May 25, 2025
-
10 Is What Percent Of 19
May 25, 2025
-
What Is 3 5 Of 60
May 25, 2025
Related Post
Thank you for visiting our website which covers about 6 Divided By What Equals 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.