56 Is What Percent Of 80
listenit
Apr 03, 2025 · 4 min read
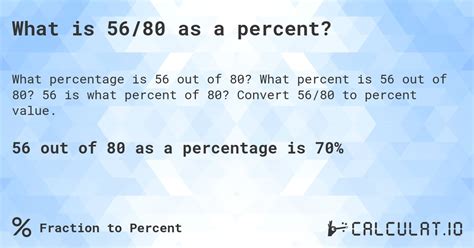
Table of Contents
56 is What Percent of 80? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This article will delve into the question, "56 is what percent of 80?", providing a detailed explanation of the calculation process, exploring different approaches, and expanding on the broader concept of percentages and their practical applications.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
To calculate percentages, we use a simple formula:
(Part / Whole) * 100% = Percentage
In our case, the "part" is 56, and the "whole" is 80. Therefore, the formula becomes:
(56 / 80) * 100% = Percentage
Calculating 56 as a Percentage of 80: The Step-by-Step Approach
Let's break down the calculation step-by-step:
-
Divide the part by the whole: 56 divided by 80 equals 0.7.
-
Multiply the result by 100: 0.7 multiplied by 100 equals 70.
-
Add the percentage symbol: This gives us the final answer: 70%.
Therefore, 56 is 70% of 80.
Alternative Methods for Calculating Percentages
While the above method is the most straightforward, there are other approaches you can use to calculate percentages, especially when dealing with more complex scenarios.
Method 2: Using Proportions
Proportions offer a powerful way to solve percentage problems. We can set up a proportion like this:
56/80 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we cross-multiply:
56 * 100 = 80 * x
5600 = 80x
x = 5600 / 80
x = 70
Therefore, x = 70%, confirming our previous result.
Method 3: Using Decimal Conversion
You can also convert the fraction to a decimal and then multiply by 100.
-
Convert the fraction 56/80 to a decimal: 56 ÷ 80 = 0.7
-
Multiply the decimal by 100: 0.7 x 100 = 70
-
Add the percentage symbol: 70%
This method highlights the direct relationship between decimals and percentages.
Real-World Applications of Percentage Calculations
Understanding percentages is crucial in many real-world situations. Here are a few examples:
1. Financial Calculations:
- Discounts: Retailers frequently offer discounts, such as "20% off." Calculating the actual discount amount requires understanding percentages. If an item costs $80 and has a 20% discount, the discount amount is (20/100) * $80 = $16.
- Taxes: Sales tax, income tax, and other taxes are often expressed as percentages. Calculating the tax amount on a purchase or income involves percentage calculations.
- Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding these rates is crucial for making informed financial decisions.
- Profit Margins: Businesses calculate profit margins as a percentage of revenue to assess profitability.
2. Data Analysis and Statistics:
- Data Representation: Percentages are used extensively in data representation, such as charts and graphs, to visualize proportions and trends.
- Statistical Analysis: Many statistical measures, such as percentages, are expressed as percentages. Understanding these measures helps interpret data and draw meaningful conclusions.
3. Everyday Life:
- Tip Calculation: Calculating a tip in a restaurant often involves calculating a percentage of the bill.
- Grade Calculation: Grades in school are often expressed as percentages, reflecting the proportion of correct answers or satisfactory performance.
- Recipe Scaling: Adjusting recipe ingredient quantities involves understanding and applying percentages.
Expanding on the Concept: Percentage Increase and Decrease
Beyond calculating what percentage one number represents of another, percentages are also used to express increases and decreases.
Percentage Increase: This calculates the increase of a value relative to its original value. The formula is:
[(New Value - Original Value) / Original Value] * 100%
Percentage Decrease: This calculates the decrease of a value relative to its original value. The formula is:
[(Original Value - New Value) / Original Value] * 100%
For example, if a stock price increases from $80 to $100, the percentage increase is:
[(100 - 80) / 80] * 100% = 25%
Troubleshooting Common Percentage Calculation Mistakes
Even simple percentage calculations can be prone to errors. Here are some common mistakes to avoid:
- Incorrect Order of Operations: Always follow the order of operations (PEMDAS/BODMAS) when performing calculations involving multiple operations.
- Mixing Decimals and Percentages: Ensure consistent use of decimals or percentages throughout the calculation. Avoid mixing them without proper conversion.
- Rounding Errors: Rounding intermediate results can lead to inaccuracies in the final answer. It's generally best to wait until the final step to round the result.
- Misunderstanding the "Whole": Clearly identify the "whole" or the total value when setting up the percentage calculation.
Conclusion: Mastering Percentage Calculations for Success
The ability to calculate percentages efficiently and accurately is a valuable skill with wide-ranging applications. Whether you are managing finances, analyzing data, or simply navigating everyday situations, a strong understanding of percentages will significantly enhance your problem-solving capabilities. By mastering the different methods and avoiding common pitfalls, you can confidently tackle percentage calculations and use them to make informed decisions in various contexts. This comprehensive guide provides the foundation for developing proficiency in this essential mathematical skill. Remember to practice regularly to reinforce your understanding and build confidence in your ability to handle percentage-related problems effectively.
Latest Posts
Latest Posts
-
Are Days Of The Week Proper Nouns
Apr 04, 2025
-
How Many Centimeters Is 70 Inches
Apr 04, 2025
-
Is An Amino Acid A Polymer
Apr 04, 2025
-
Calculating Square Inches Of A Circle
Apr 04, 2025
-
Does Sohcahtoa Only Work On Right Triangles
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about 56 Is What Percent Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
