Does Sohcahtoa Only Work On Right Triangles
listenit
Apr 04, 2025 · 5 min read
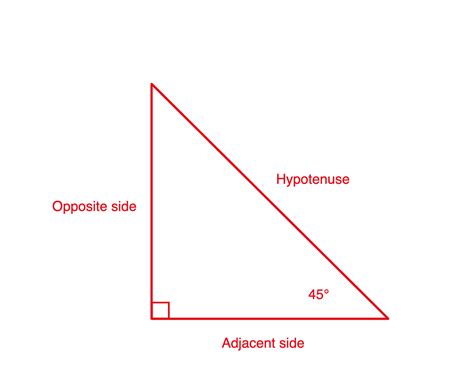
Table of Contents
Does SOHCAHTOA Only Work on Right Triangles?
SOHCAHTOA, the mnemonic device for remembering the trigonometric ratios (Sine, Cosine, Tangent), is a cornerstone of introductory trigonometry. But a common question arises: does SOHCAHTOA only work on right triangles? The short answer is yes, in its most basic form. However, the underlying principles of trigonometry extend far beyond right triangles, allowing us to solve problems involving any type of triangle. This article delves into the intricacies of SOHCAHTOA, exploring its limitations and showcasing how more advanced trigonometric concepts build upon its foundation to handle a broader range of problems.
Understanding SOHCAHTOA
Let's refresh our understanding of SOHCAHTOA. It's a mnemonic to remember the definitions of the three primary trigonometric functions for right-angled triangles:
- SOH: Sine = Opposite / Hypotenuse
- CAH: Cosine = Adjacent / Hypotenuse
- TOA: Tangent = Opposite / Adjacent
Here, "opposite," "adjacent," and "hypotenuse" refer to the sides of a right-angled triangle relative to a specific angle. The hypotenuse is always the longest side, opposite the right angle. The opposite side is the side directly across from the angle in question, and the adjacent side is the side next to the angle (but not the hypotenuse).
Example: In a right-angled triangle with an angle θ, if the opposite side has length 3 and the hypotenuse has length 5, then sin(θ) = 3/5.
Why SOHCAHTOA is Restricted to Right Triangles
SOHCAHTOA's reliance on the right angle is fundamental. The definitions themselves depend on the concept of a hypotenuse, a side unique to right-angled triangles. Without a right angle, we don't have a hypotenuse, and therefore, the ratios defined by SOHCAHTOA lose their meaning. The "opposite" and "adjacent" sides also require the reference point of the right angle to be precisely defined.
In essence, SOHCAHTOA is a shortcut, a simplified way to understand trigonometric ratios within a specific geometric context—the right-angled triangle. This makes it exceptionally useful for solving many practical problems, from calculating building heights to determining distances in surveying. However, its limitations become apparent when dealing with triangles that don't possess a right angle.
Extending Trigonometry Beyond Right Triangles: The Law of Sines and Cosines
To handle non-right-angled triangles (oblique triangles), we need more sophisticated tools: the Law of Sines and the Law of Cosines. These laws provide powerful methods for solving for unknown angles and sides in any triangle, regardless of whether it contains a right angle.
The Law of Sines
The Law of Sines states that the ratio of the length of a side to the sine of its opposite angle is constant for all three sides of a triangle:
a/sin(A) = b/sin(B) = c/sin(C)
where 'a', 'b', and 'c' are the lengths of the sides, and 'A', 'B', and 'C' are the angles opposite those sides respectively.
This law is particularly useful when you know two angles and one side (ASA or AAS), or two sides and one opposite angle (SSA – but be aware of the ambiguous case).
The Law of Cosines
The Law of Cosines generalizes the Pythagorean theorem to non-right-angled triangles. It relates the lengths of the sides to the cosine of one of the angles:
a² = b² + c² - 2bc * cos(A)
This law is invaluable when you know two sides and the included angle (SAS) or when you know all three sides (SSS).
Unit Circle and Trigonometric Functions Beyond Triangles
The power of trigonometric functions extends far beyond their geometric interpretations in triangles. The unit circle, a circle with a radius of 1 centered at the origin of a coordinate plane, provides a more comprehensive framework.
By considering the coordinates of points on the unit circle, we can define trigonometric functions for any angle, not just those within a right-angled triangle. For an angle θ measured counterclockwise from the positive x-axis:
- cos(θ) is the x-coordinate of the point on the unit circle.
- sin(θ) is the y-coordinate of the point on the unit circle.
- tan(θ) is the ratio sin(θ)/cos(θ) (and is undefined where cos(θ) = 0).
This representation allows us to define trigonometric functions for angles greater than 90 degrees, negative angles, and even angles exceeding 360 degrees (through cyclical repetition). This expanded definition seamlessly integrates with the Laws of Sines and Cosines, allowing us to apply trigonometry universally.
Applications Beyond Basic Triangles
The expanded understanding of trigonometry finds applications in diverse fields:
- Navigation: Determining positions, distances, and bearings using angles and distances.
- Surveying: Mapping land areas, calculating areas, and determining heights.
- Engineering: Designing structures, analyzing forces, and modeling complex systems.
- Physics: Analyzing projectile motion, wave phenomena, and oscillatory systems.
- Computer Graphics: Modeling 3D objects, rendering scenes, and manipulating images.
SOHCAHTOA's Role in Advanced Trigonometry
While SOHCAHTOA itself is limited to right-angled triangles, its underlying concepts are crucial building blocks for understanding the more general laws of trigonometry. The intuitive understanding of ratios – opposite/hypotenuse, adjacent/hypotenuse, and opposite/adjacent – provides a solid foundation for grasping the more abstract formulations of the Law of Sines and Cosines. Furthermore, SOHCAHTOA is often used to solve for parts of right-angled triangles within larger, more complex problems involving oblique triangles.
Conclusion
In conclusion, the straightforward mnemonic SOHCAHTOA is a helpful tool for solving problems involving right-angled triangles. However, its application is limited to this specific type of triangle. The true power of trigonometry lies in its ability to handle any triangle, utilizing the Law of Sines and the Law of Cosines. Furthermore, the unit circle provides an even broader perspective, extending the definition of trigonometric functions beyond the confines of triangles and paving the way for applications in a vast array of fields. While SOHCAHTOA serves as a valuable introductory concept, it's crucial to recognize its limitations and embrace the wider scope of trigonometric principles to tackle a broader range of geometric and mathematical problems. The journey beyond SOHCAHTOA opens up a world of mathematical possibilities, solidifying its place as a fundamental yet limited stepping stone in the expansive realm of trigonometry.
Latest Posts
Latest Posts
-
Simplify The Square Root Of 27
Apr 04, 2025
-
22 Is What Percent Of 55
Apr 04, 2025
-
1 Degree Celsius Equals How Many Fahrenheit
Apr 04, 2025
-
How Many Combinatos Of 5 Letters
Apr 04, 2025
-
How Many Chambers Does The Amphibian Heart Have
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Does Sohcahtoa Only Work On Right Triangles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
