50 Of 250 Is What Percent
listenit
May 25, 2025 · 4 min read
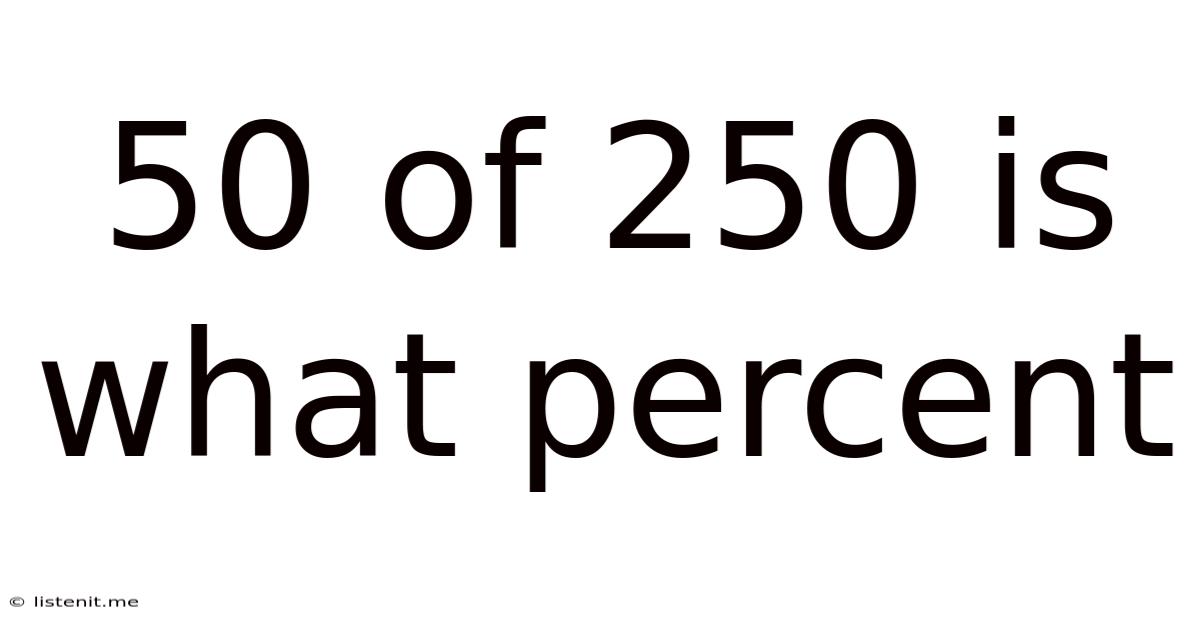
Table of Contents
50 out of 250 is What Percent? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide will not only answer the question, "50 out of 250 is what percent?" but also equip you with the knowledge and tools to tackle similar percentage problems with confidence. We'll delve into the methods, explore practical applications, and offer tips for mastering percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "percent," which literally means "out of 100." Therefore, 50% is equivalent to 50/100, or 1/2, or 0.5 in decimal form.
Calculating "50 out of 250 is What Percent?"
There are several ways to calculate the percentage that 50 represents when compared to 250. Let's explore the most common methods:
Method 1: Using the Proportion Method
This method utilizes the fundamental concept of proportions. We set up a proportion where 'x' represents the unknown percentage:
50/250 = x/100
To solve for 'x', we cross-multiply:
50 * 100 = 250 * x
5000 = 250x
Now, divide both sides by 250:
x = 5000 / 250
x = 20
Therefore, 50 out of 250 is 20%.
Method 2: Using Decimal Conversion
This method involves converting the fraction 50/250 into a decimal and then multiplying by 100 to express it as a percentage.
-
Convert the fraction to a decimal: 50 ÷ 250 = 0.2
-
Multiply the decimal by 100: 0.2 * 100 = 20
Therefore, 50 out of 250 is 20%.
Method 3: Using the Percentage Formula
The basic percentage formula is:
(Part / Whole) * 100 = Percentage
In our case:
(50 / 250) * 100 = 20%
This formula directly calculates the percentage by dividing the part (50) by the whole (250) and then multiplying by 100.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world scenarios. Here are some examples:
1. Discount Calculations:
Imagine a shirt originally priced at $250 is on sale for $50 off. To determine the discount percentage, we use the percentage formula:
(50 / 250) * 100 = 20%
The shirt is discounted by 20%.
2. Grade Calculation:
If a student scores 50 points out of a possible 250 points on an exam, their percentage score is:
(50 / 250) * 100 = 20%
The student achieved a 20% on the exam.
3. Sales and Commission:
A salesperson who makes 50 sales out of 250 potential clients has a success rate of:
(50 / 250) * 100 = 20%
Their sales conversion rate is 20%.
4. Financial Analysis:
Investors use percentages to analyze returns on investments, growth rates, and other financial metrics. For example, if an investment grows from $200 to $250, the percentage increase is:
((250 - 200) / 200) * 100 = 25%
The investment grew by 25%.
5. Data Analysis and Statistics:
Percentages are frequently used to represent proportions within datasets, making it easier to visualize and interpret data. For example, if 50 out of 250 survey respondents answered "yes" to a particular question, the percentage of "yes" responses is 20%.
Tips for Mastering Percentage Calculations
- Practice regularly: The more you practice, the more comfortable and proficient you'll become with percentage calculations.
- Understand the concepts: Ensure you grasp the fundamental concepts of fractions, decimals, and proportions, as they are essential to understanding percentages.
- Use different methods: Try different calculation methods to find the approach that works best for you.
- Check your work: Always double-check your calculations to minimize errors.
- Use calculators and online tools: Utilize calculators and online tools when necessary, especially for more complex percentage problems.
- Break down complex problems: If you encounter a complex percentage problem, break it down into smaller, manageable steps.
Beyond the Basics: Advanced Percentage Applications
While calculating "50 out of 250 is what percent?" might seem simple, understanding percentages extends far beyond basic calculations. Advanced applications involve:
- Compound interest: Calculating interest earned on both the principal and accumulated interest.
- Percentage change: Determining the percentage increase or decrease between two values.
- Percentage points: Understanding the difference between a percentage change and a percentage point change.
- Statistical analysis: Using percentages in hypothesis testing, confidence intervals, and other statistical methods.
Conclusion: Mastering the Power of Percentages
This guide comprehensively addressed the question, "50 out of 250 is what percent?" demonstrating various calculation methods and highlighting its practical applications across numerous fields. By understanding and mastering percentage calculations, you enhance your problem-solving skills and develop a valuable tool applicable to various aspects of personal and professional life. Remember to practice consistently and explore different approaches to solidify your understanding and build confidence in tackling percentage problems of any complexity. The ability to calculate and interpret percentages is a powerful skill that will undoubtedly benefit you in numerous ways.
Latest Posts
Latest Posts
-
4 13 20 As A Decimal
May 25, 2025
-
2pm To 2pm The Next Day Is How Many Hours
May 25, 2025
-
28 Days From Today Will Be
May 25, 2025
-
8 Out Of 21 As A Percentage
May 25, 2025
-
How Many Times Does 2 Go Into 5
May 25, 2025
Related Post
Thank you for visiting our website which covers about 50 Of 250 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.