50 Is 80 Of What Number
listenit
May 11, 2025 · 5 min read
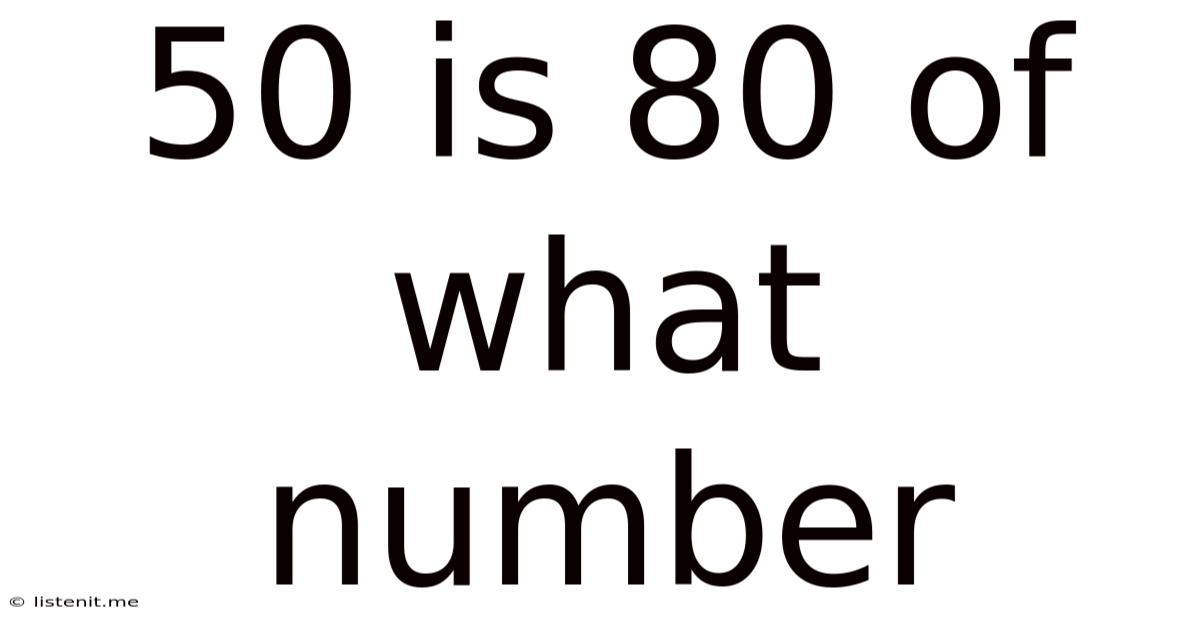
Table of Contents
50 is 80% of What Number? A Deep Dive into Percentage Calculations
Welcome to a comprehensive exploration of percentage calculations, focusing specifically on the question: "50 is 80% of what number?" This seemingly simple question opens the door to understanding fundamental mathematical concepts applicable across various fields, from finance and statistics to everyday life. We will delve into different methods of solving this problem, discuss the underlying principles, and provide practical examples to solidify your understanding. By the end, you'll not only know the answer but also possess a strong foundation for tackling similar percentage problems with confidence.
Understanding Percentages
Before diving into the solution, let's refresh our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred." For example, 80% means 80 out of 100, or 80/100, which simplifies to 4/5 or 0.8 as a decimal.
This understanding is crucial because percentage problems often involve translating words into mathematical equations. The phrase "50 is 80% of what number" can be translated into an algebraic equation that we can then solve.
Method 1: Setting up an Equation
The most straightforward approach involves setting up an algebraic equation. Let's represent the unknown number as "x." We can then translate the problem into the following equation:
50 = 0.8x
Here, 0.8 represents 80% expressed as a decimal. To solve for x, we simply need to isolate x by dividing both sides of the equation by 0.8:
x = 50 / 0.8
x = 62.5
Therefore, 50 is 80% of 62.5.
Method 2: Using Proportions
Another effective method involves using proportions. A proportion is a statement of equality between two ratios. We can set up a proportion as follows:
50/x = 80/100
Here, 50 represents the part, x represents the whole, and 80/100 represents the percentage. To solve this proportion, we can cross-multiply:
50 * 100 = 80 * x
5000 = 80x
Now, we divide both sides by 80 to isolate x:
x = 5000 / 80
x = 62.5
Again, we arrive at the same answer: 50 is 80% of 62.5.
Method 3: Using the Percentage Formula
The percentage formula provides a more generalized approach to solving percentage problems. The formula is:
Part = Percentage × Whole
In our problem:
- Part = 50
- Percentage = 80% = 0.8
- Whole = x (the unknown number)
Substituting these values into the formula, we get:
50 = 0.8 × x
Solving for x (by dividing both sides by 0.8), we obtain:
x = 50 / 0.8
x = 62.5
This method reinforces the consistency of our answer: 50 is 80% of 62.5.
Practical Applications and Real-World Examples
Understanding percentage calculations is essential in numerous real-world scenarios. Let's consider a few examples:
1. Sales and Discounts: Imagine a store offering an 80% discount on an item. If the discounted price is $50, we can use the same methods to determine the original price. Using the equation:
50 = 0.2x (where 0.2 represents the remaining 20% after the 80% discount)
x = 50 / 0.2 = $250
The original price of the item was $250.
2. Financial Calculations: Percentage calculations are fundamental in finance. For example, calculating interest earned on an investment, determining profit margins, or understanding loan repayments often requires working with percentages.
3. Statistics and Data Analysis: Percentages are widely used in statistics to represent proportions, frequencies, and probabilities. Understanding how to calculate percentages is crucial for interpreting data and making informed decisions based on statistical analysis.
4. Everyday Life: From calculating tips in restaurants to understanding tax rates, percentages are embedded in our daily lives. The ability to quickly and accurately calculate percentages makes everyday financial decisions simpler and more efficient.
Expanding Your Understanding: Variations on the Theme
While we've focused on "50 is 80% of what number," let's briefly consider variations to solidify your grasp on percentage problems:
- What is 80% of 62.5? This is a straightforward calculation: 0.8 * 62.5 = 50.
- What percentage of 62.5 is 50? This involves calculating (50/62.5) * 100% = 80%.
- If 50 represents 80%, what would 100% represent? This problem can be solved using proportions or the percentage formula, leading to the answer 62.5.
These variations highlight the interconnectedness of percentage calculations and illustrate how a change in the given information alters the problem-solving approach, yet consistently leads to the same underlying relationship between the numbers.
Mastering Percentage Calculations: Tips and Strategies
Here are some strategies to improve your proficiency in solving percentage problems:
- Understand the vocabulary: Familiarize yourself with the terms "percent," "of," "is," and "what number." These words are key to translating word problems into mathematical equations.
- Practice regularly: The more you practice solving percentage problems, the more comfortable and proficient you will become. Start with simple problems and gradually increase the difficulty.
- Use different methods: Explore various approaches—equations, proportions, and the percentage formula—to solidify your understanding and find the method that best suits your style.
- Check your answers: After solving a problem, always check your answer to ensure accuracy. You can do this by substituting your answer back into the original problem.
- Utilize online resources: Numerous websites and educational platforms offer free resources and practice problems to help you improve your skills.
Conclusion: Beyond the Numbers
This comprehensive exploration of "50 is 80% of what number?" has gone beyond simply providing the answer (62.5). We've dissected the underlying principles of percentage calculations, explored different solution methods, and demonstrated their practical applications in diverse contexts. By mastering percentage calculations, you're not just acquiring a mathematical skill, but also developing a powerful tool applicable to various aspects of your personal and professional life. Remember to practice consistently and embrace different approaches to truly internalize this crucial mathematical concept. The ability to confidently navigate percentage problems will serve you well in countless situations.
Latest Posts
Latest Posts
-
When To Use A Semicolon With However
May 12, 2025
-
Write The Complete Ground State Electron Configuration Of C
May 12, 2025
-
Does Methanol Have Dipole Dipole Forces
May 12, 2025
-
How To Find Volume And Mass From Density
May 12, 2025
-
What Is The Mixed Number For 7 5
May 12, 2025
Related Post
Thank you for visiting our website which covers about 50 Is 80 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.