5 Divided By 2 As A Fraction
listenit
May 24, 2025 · 5 min read
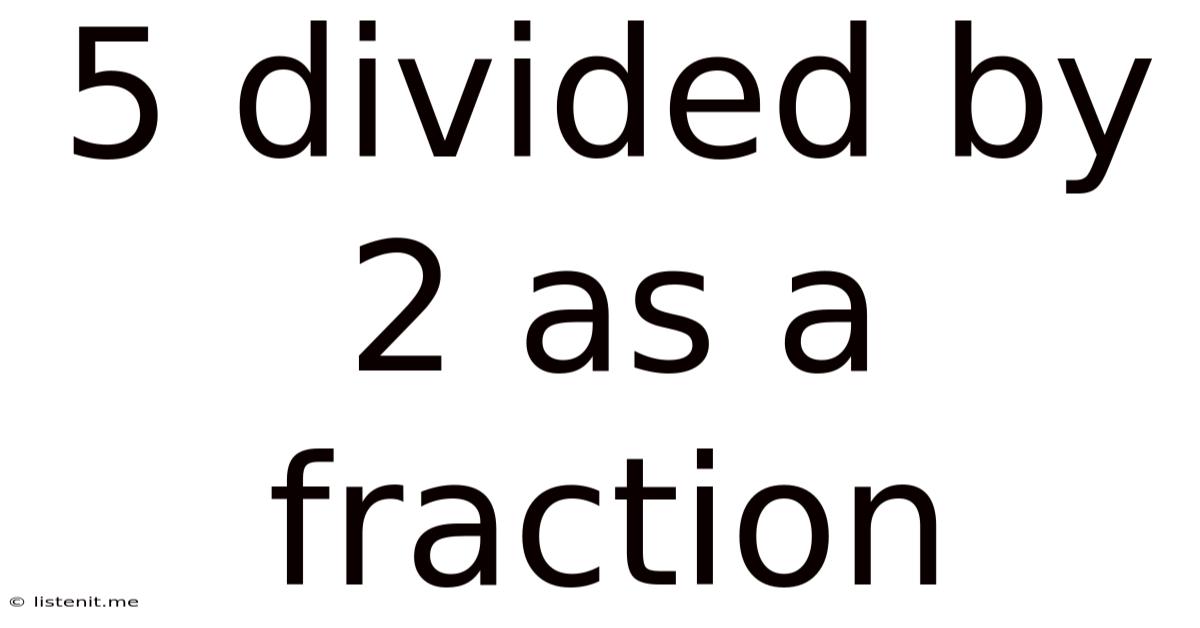
Table of Contents
5 Divided by 2 as a Fraction: A Comprehensive Guide
Dividing 5 by 2 might seem like a simple arithmetic problem, but it offers a great opportunity to delve into the world of fractions and their practical applications. This comprehensive guide will explore various methods of representing 5 divided by 2 as a fraction, explaining the underlying concepts and demonstrating their relevance in different contexts. We'll move beyond the simple answer and examine the nuances of fractions, including their simplification, decimal equivalents, and real-world uses.
Understanding Fractions: The Building Blocks
Before diving into the specifics of 5 divided by 2, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key elements:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction ¾, the numerator (3) represents the number of parts we possess, while the denominator (4) represents the total number of equal parts the whole is divided into.
Representing 5 Divided by 2 as a Fraction
The division problem "5 divided by 2" can be directly translated into a fraction:
5/2
This fraction means that we have 5 parts out of a total of 2 equal parts. While this might seem counterintuitive (how can you have 5 parts out of only 2?), it's perfectly valid in the world of mathematics. This represents an improper fraction, where the numerator is larger than the denominator.
Improper Fractions vs. Mixed Numbers
Improper fractions, like 5/2, are perfectly acceptable and often necessary for calculations. However, they can also be expressed as mixed numbers. A mixed number combines a whole number and a proper fraction (where the numerator is smaller than the denominator).
To convert 5/2 into a mixed number, we perform the division:
5 ÷ 2 = 2 with a remainder of 1
This means that 5/2 contains two whole units and one remaining part out of two. Therefore, 5/2 can be written as:
2 ½
Both 5/2 and 2 ½ represent the same value; they are simply different ways of expressing it. The choice between using an improper fraction or a mixed number often depends on the context of the problem and personal preference. In many mathematical calculations, improper fractions are preferred for their ease of manipulation.
Simplifying Fractions
Fractions can often be simplified by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. However, in the case of 5/2, the GCD of 5 and 2 is 1. Therefore, 5/2 is already in its simplest form. This means we cannot reduce the fraction further while maintaining its value.
Decimal Equivalents
Fractions can also be represented as decimals. To find the decimal equivalent of 5/2, we simply perform the division:
5 ÷ 2 = 2.5
Therefore, 5/2 is equal to 2.5. This decimal representation is often useful for practical applications, especially when dealing with measurements or monetary values.
Real-World Applications of 5/2
The fraction 5/2, or its equivalent 2.5, appears in various real-world scenarios:
- Sharing: If you have 5 pizzas to share equally among 2 people, each person receives 2 ½ pizzas.
- Measurement: If you have a piece of wood that is 5 meters long and you need to cut it into 2 equal pieces, each piece will be 2.5 meters long.
- Finance: If you split a $5 bill equally between two people, each person receives $2.50.
- Recipes: Many baking recipes utilize fractions. If a recipe calls for 5 cups of flour and you want to halve the recipe, you will need 2 ½ cups of flour.
These examples showcase the practical relevance of understanding and working with fractions like 5/2. The ability to convert between fractions, mixed numbers, and decimals provides flexibility in solving various problems.
Further Exploration of Fractions
Understanding 5/2 as a fraction provides a springboard to explore more complex fractional concepts:
Adding and Subtracting Fractions:
Adding and subtracting fractions requires a common denominator. For example, adding 5/2 and 3/4 would involve finding a common denominator (4) and rewriting the fractions accordingly before performing the addition.
Multiplying and Dividing Fractions:
Multiplying fractions involves multiplying the numerators and multiplying the denominators. Dividing fractions involves inverting the second fraction and then multiplying. These operations are fundamental to various mathematical fields.
Working with Negative Fractions:
Negative fractions simply indicate a negative value. Rules for operating with negative fractions follow the same principles as operating with positive fractions, with the added consideration of signs.
Fractions and Ratios:
Fractions are closely related to ratios. A ratio is a comparison between two quantities, often expressed in the form a:b or a/b. Understanding fractions strengthens one's understanding of ratios and proportions.
Fractions in Algebra:
Fractions play a significant role in algebra, appearing in equations, expressions, and functions. The ability to manipulate fractions is crucial for solving algebraic problems.
Conclusion: Mastering the Fraction 5/2 and Beyond
While initially seeming straightforward, the simple division of 5 by 2 opens a gateway to a rich understanding of fractions, their properties, and their widespread applications. By grasping the various representations of 5/2 (as an improper fraction, a mixed number, and a decimal), and understanding the principles of fraction simplification and conversion, you equip yourself with a fundamental skill set applicable across numerous mathematical and real-world contexts. The exploration of fractions extends far beyond this single example, forming a cornerstone of mathematical literacy and problem-solving abilities. Continuous practice and exploration of different fractional scenarios will solidify your understanding and confidence in working with fractions. This foundational understanding will pave the way for tackling more complex mathematical challenges. The journey from understanding 5/2 to mastering the broader world of fractions is an enriching and empowering one, enabling you to approach problems with clarity, precision, and confidence.
Latest Posts
Latest Posts
-
4 7 9 As An Improper Fraction
May 25, 2025
-
4 Divided By 7 As A Fraction
May 25, 2025
-
What Percentage Is 4 Out Of 12
May 25, 2025
-
What Is The Greatest Common Factor Of 85 And 51
May 25, 2025
-
What Is 8 Weeks Ago From Today
May 25, 2025
Related Post
Thank you for visiting our website which covers about 5 Divided By 2 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.