5 9 Divided By 5 As A Fraction
listenit
May 23, 2025 · 4 min read
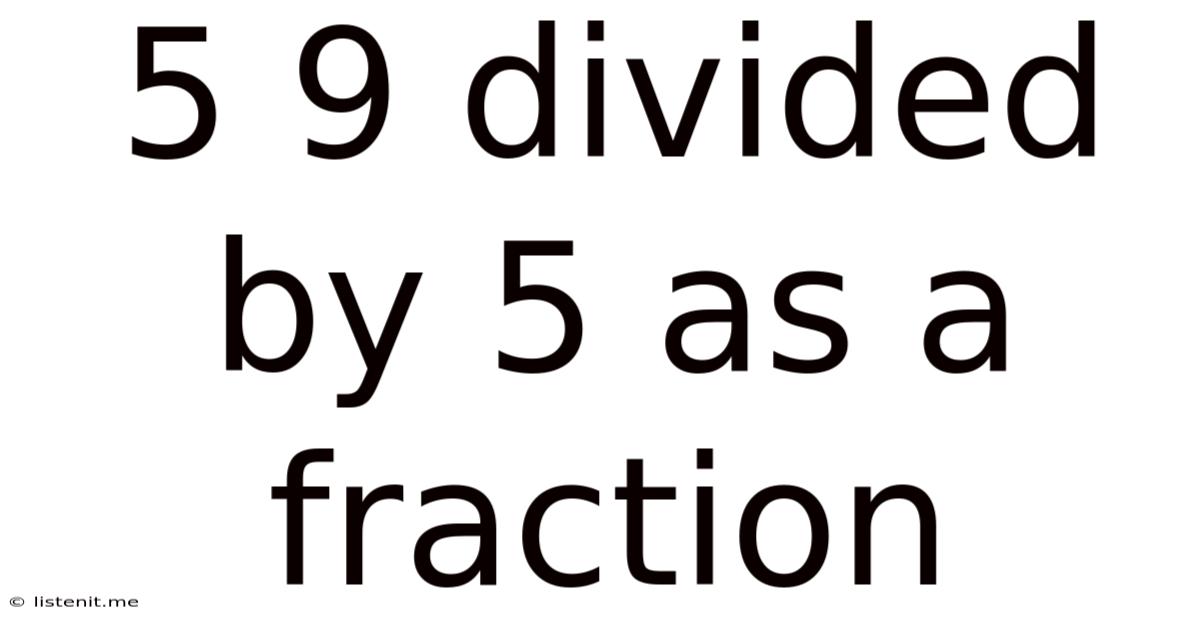
Table of Contents
5 9/5 as a Fraction: A Comprehensive Guide
This article delves into the intricacies of converting the mixed number 5 9/5 into a fraction. We'll explore the underlying mathematical principles, provide step-by-step instructions, and offer various approaches to solve this problem. We'll also address common misconceptions and offer helpful tips for future fraction conversions. This comprehensive guide aims to solidify your understanding of fraction manipulation and improve your mathematical skills.
Understanding Mixed Numbers and Improper Fractions
Before we begin the conversion, let's define our terms. A mixed number combines a whole number and a fraction, such as 5 9/5. An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). Converting a mixed number to a fraction involves transforming it into an equivalent improper fraction.
Why Convert to an Improper Fraction?
Improper fractions are essential in many mathematical operations, particularly when adding, subtracting, multiplying, and dividing fractions. They provide a consistent and streamlined approach to these calculations, eliminating the need for separate handling of whole numbers and fractional parts. This consistency simplifies calculations and reduces the chance of errors.
Method 1: Converting 5 9/5 to an Improper Fraction
This method utilizes a straightforward formula to convert a mixed number to an improper fraction.
Step 1: Multiply the whole number by the denominator.
In our example, the whole number is 5, and the denominator is 5. Multiplying these gives us 5 * 5 = 25.
Step 2: Add the numerator to the result from Step 1.
Our numerator is 9. Adding this to the result from Step 1, we get 25 + 9 = 34.
Step 3: Keep the denominator the same.
The denominator remains 5.
Step 4: Write the improper fraction.
Combining the results from Steps 2 and 3, we get the improper fraction 34/5.
Therefore, 5 9/5 = 34/5.
Method 2: Visualizing the Conversion
This method uses a visual approach to understand the conversion process. Imagine 5 whole units, each divided into 5 equal parts. This represents the whole number 5 in fractional terms (5/5 + 5/5 + 5/5 + 5/5 + 5/5). Now, add the additional 9/5.
Visualizing this: we have 5 whole units, each composed of 5 fifths. That's a total of 25 fifths (5 * 5 = 25). Adding the additional 9 fifths (9/5) gives us a total of 34 fifths (25 + 9 = 34). This reinforces the result: 34/5.
Method 3: Understanding the Underlying Principle
The conversion process is based on the fundamental principle that a whole number can be expressed as a fraction with any denominator. For instance, 5 can be expressed as 5/1, 10/2, 15/3, 25/5, and so on. In our case, we choose the denominator 5 to maintain consistency with the fractional part of the mixed number. This allows us to add the fractional parts directly.
Simplifying Improper Fractions
While 34/5 is a perfectly valid improper fraction, sometimes it's beneficial to simplify it further. Simplifying means reducing the fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it. In this case, the GCD of 34 and 5 is 1. Since the GCD is 1, the fraction is already in its simplest form.
Applications of Improper Fractions
Improper fractions are widely used in various applications:
- Cooking and Baking: Recipes often require fractional measurements, and improper fractions ensure precise calculations.
- Construction and Engineering: Precise measurements are critical, and improper fractions simplify calculations.
- Finance and Accounting: Calculating proportions and ratios frequently involves improper fractions.
- Computer Science: Data structures and algorithms often utilize fractional representations.
- Everyday Life: Dividing things equally or making precise measurements often requires dealing with fractions.
Common Mistakes to Avoid
- Incorrectly adding the whole number and the numerator: Remember to multiply the whole number by the denominator before adding the numerator.
- Forgetting to keep the denominator the same: The denominator remains unchanged throughout the conversion process.
- Not simplifying the resulting improper fraction: Always check if the resulting improper fraction can be simplified to its lowest terms.
Further Practice Problems
To reinforce your understanding, try converting the following mixed numbers to improper fractions:
- 3 2/3
- 7 5/8
- 1 11/12
- 10 3/4
- 2 9/10
By working through these examples, you'll solidify your grasp of the conversion process and improve your comfort level with working with fractions.
Conclusion
Converting the mixed number 5 9/5 to the improper fraction 34/5 is a fundamental skill in mathematics. Understanding the underlying principles and employing the step-by-step method ensures accurate and efficient conversion. Remember to avoid common errors, practice regularly, and appreciate the versatility and importance of improper fractions in various applications. Mastering fraction conversion is a cornerstone of mathematical proficiency. This comprehensive guide provided diverse approaches and reinforces your understanding of this essential mathematical concept. Now, you're equipped to confidently tackle similar problems and continue your journey in mathematics with enhanced skills and knowledge.
Latest Posts
Latest Posts
-
30 Days From September 19 2024
May 23, 2025
-
How Do You Figure Out Your Gas Mileage
May 23, 2025
-
What Time Will It Be 18 Minutes From Now
May 23, 2025
-
3 8 Divided By 2 As A Fraction
May 23, 2025
-
30 Days From Feb 16 2024
May 23, 2025
Related Post
Thank you for visiting our website which covers about 5 9 Divided By 5 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.