3/8 Divided By 2 As A Fraction
listenit
May 23, 2025 · 5 min read
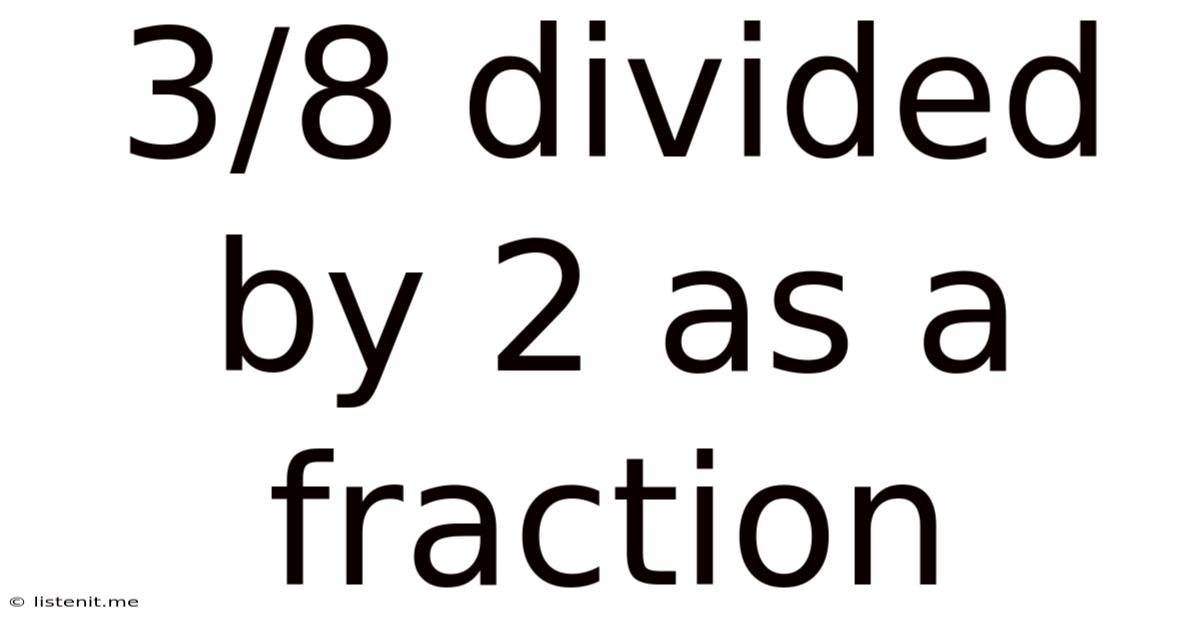
Table of Contents
3/8 Divided by 2: A Deep Dive into Fraction Division
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes surprisingly straightforward. This comprehensive guide will walk you through dividing 3/8 by 2, explaining the underlying principles and providing multiple approaches to solve this problem. We'll also explore related concepts and practical applications to solidify your understanding of fraction division.
Understanding Fraction Division
Before tackling 3/8 divided by 2, let's review the fundamental concept of dividing fractions. Dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2. This crucial concept forms the basis of our solution.
The Reciprocal: The Key to Fraction Division
The reciprocal, also known as the multiplicative inverse, is a number that, when multiplied by the original number, results in 1. For fractions, finding the reciprocal is as easy as swapping the numerator and the denominator.
- Example: The reciprocal of 5/7 is 7/5. (5/7 * 7/5 = 1)
- Whole Numbers as Fractions: Remember that whole numbers can be expressed as fractions with a denominator of 1. For example, 2 can be written as 2/1. This will be vital when dealing with whole numbers in fraction division problems.
Solving 3/8 Divided by 2
Now, let's apply this knowledge to solve the problem: 3/8 divided by 2.
Step 1: Rewrite the whole number as a fraction.
As mentioned earlier, we rewrite 2 as a fraction: 2/1. Our problem now looks like this: (3/8) ÷ (2/1).
Step 2: Change the division to multiplication by using the reciprocal.
The crucial step is to replace the division sign with a multiplication sign and use the reciprocal of the second fraction (2/1). The reciprocal of 2/1 is 1/2. Our equation transforms into: (3/8) x (1/2).
Step 3: Multiply the numerators and denominators.
Multiply the numerators together (3 x 1 = 3) and the denominators together (8 x 2 = 16). This gives us the result: 3/16.
Therefore, 3/8 divided by 2 is equal to 3/16.
Alternative Methods and Visual Representations
While the reciprocal method is the most efficient, other methods can help visualize the process and reinforce understanding.
Visualizing with Fraction Bars
Imagine a rectangular bar representing 3/8. Dividing this by 2 means splitting this 3/8 bar into two equal parts. Each resulting part will represent 3/16 of the whole. This visual representation can be particularly helpful for beginners.
Repeated Subtraction
Another approach, though less efficient for larger numbers, involves repeated subtraction. How many times can you subtract 2/1 from 3/8? This method highlights the concept of division as repeated subtraction but can be complex and less practical for more complex problems. It's useful for conceptual understanding but not for practical, efficient calculation.
Practical Applications and Real-World Examples
Understanding fraction division isn't just an academic exercise. It has many practical applications in everyday life:
- Cooking and Baking: Scaling recipes up or down requires dividing fractions. If a recipe calls for 3/8 cup of sugar and you want to halve it, you need to divide 3/8 by 2.
- Construction and Measurement: Precise measurements in construction frequently involve fractions. Dividing fractional measurements is essential for accurate work.
- Sewing and Crafts: Similar to construction, many crafts require precise fractional measurements, demanding an understanding of fraction division.
- Data Analysis: When dealing with proportions and percentages, especially in smaller datasets, understanding fraction division helps in accurate interpretation of results.
Expanding on Fraction Division: More Complex Scenarios
While we've focused on 3/8 divided by 2, let's explore more complex scenarios to further solidify your understanding of fraction division.
Dividing Fractions by Fractions
Let's consider dividing a fraction by another fraction. For example: (5/6) ÷ (2/3).
- Find the reciprocal of the second fraction: The reciprocal of 2/3 is 3/2.
- Multiply the fractions: (5/6) x (3/2) = (5 x 3) / (6 x 2) = 15/12
- Simplify the result: 15/12 simplifies to 5/4 or 1 1/4.
Dividing Mixed Numbers
Mixed numbers, like 1 1/2, can also be involved in division problems. The first step here is to convert the mixed number into an improper fraction.
For example, (1 1/2) ÷ (1/4):
- Convert to improper fraction: 1 1/2 becomes 3/2.
- Find the reciprocal: The reciprocal of 1/4 is 4/1 (or simply 4).
- Multiply: (3/2) x (4/1) = 12/2 = 6
Dividing by a Decimal
Sometimes, you might encounter problems involving the division of a fraction by a decimal. To solve these, convert the decimal to a fraction first.
For example, (1/2) ÷ 0.25:
- Convert 0.25 to a fraction: 0.25 is equivalent to 1/4.
- Find the reciprocal: The reciprocal of 1/4 is 4/1 (or 4).
- Multiply: (1/2) x (4/1) = 4/2 = 2
Troubleshooting Common Mistakes
Even with a clear understanding, errors can creep in. Here are some common mistakes to watch out for:
- Forgetting the reciprocal: This is the most common error. Remember to always use the reciprocal of the second fraction when changing division to multiplication.
- Incorrectly simplifying fractions: Always simplify your answer to its lowest terms.
- Mistakes in multiplication: Double-check your multiplication of numerators and denominators to avoid errors.
- Not converting mixed numbers: Before performing division, ensure all mixed numbers are converted to improper fractions.
Conclusion: Mastering Fraction Division
Mastering fraction division opens doors to a deeper understanding of mathematics and its practical applications. By understanding the concept of reciprocals and following the steps outlined above, you can confidently tackle any fraction division problem, from the simple (like 3/8 divided by 2) to the more complex scenarios involving mixed numbers and decimals. Remember to practice regularly to build fluency and confidence in your abilities. With consistent effort, fraction division will become second nature.
Latest Posts
Latest Posts
-
What Percent Of 11 Is 3
May 23, 2025
-
1949 To 2023 How Many Years
May 23, 2025
-
2 Hours 40 Minutes From Now
May 23, 2025
-
How Many Points Do I Get On Ww
May 23, 2025
-
9 Divided By 6 As A Fraction
May 23, 2025
Related Post
Thank you for visiting our website which covers about 3/8 Divided By 2 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.