What Percent Of 11 Is 3
listenit
May 23, 2025 · 4 min read
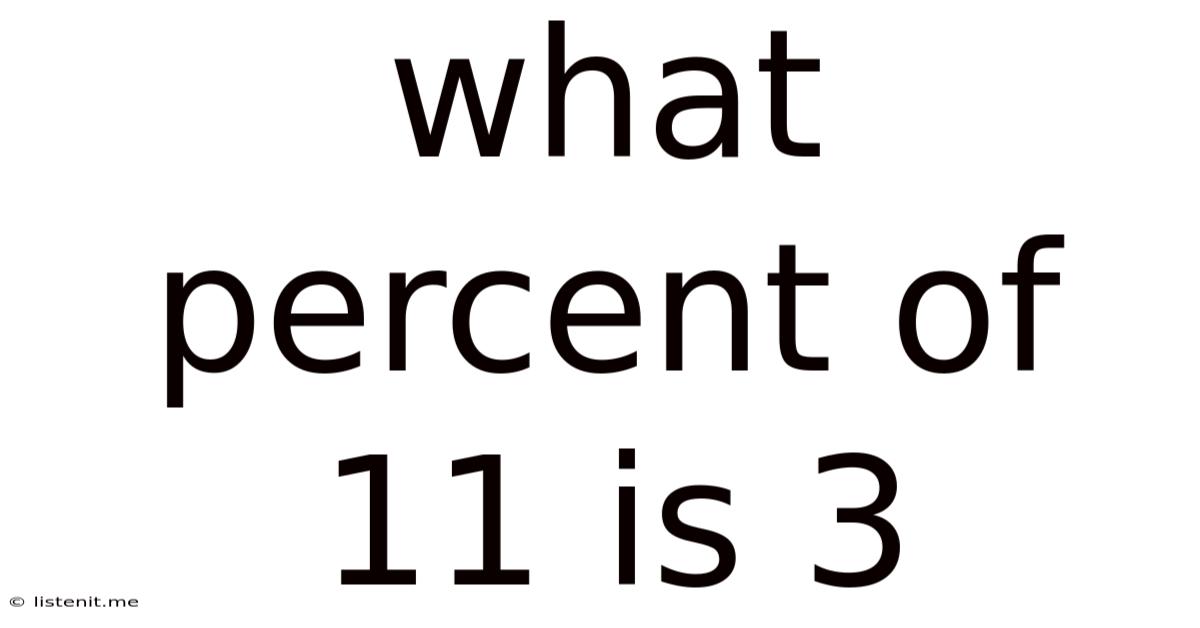
Table of Contents
What Percent of 11 is 3? A Deep Dive into Percentage Calculations
Finding what percent of 11 is 3 might seem like a simple problem, but understanding the underlying principles unlocks a world of practical applications in various fields. This comprehensive guide will not only solve this specific problem but will also equip you with the knowledge and skills to tackle similar percentage calculations with ease. We'll explore different methods, delve into the underlying mathematical concepts, and discuss real-world examples where such calculations are essential.
Understanding Percentages: The Foundation
Before diving into the solution, let's solidify our understanding of percentages. A percentage is a fraction expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100". For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Key Concepts:
- Part: This represents the specific amount we're interested in. In our problem, the part is 3.
- Whole: This represents the total amount. In our problem, the whole is 11.
- Percentage: This is the fraction of the whole represented as a number out of 100. This is what we need to find.
Method 1: The Formula Approach
The most straightforward method involves using a simple formula:
(Part / Whole) * 100 = Percentage
Let's apply this to our problem:
(3 / 11) * 100 = Percentage
Calculating this:
0.2727 * 100 ≈ 27.27%
Therefore, 3 is approximately 27.27% of 11.
Method 2: Proportion Method
This method utilizes the concept of proportions. We can set up a proportion to solve for the unknown percentage (x):
3/11 = x/100
To solve for x, we cross-multiply:
11x = 300
x = 300 / 11
x ≈ 27.27
Therefore, again, we find that 3 is approximately 27.27% of 11.
Method 3: Using Decimal Conversion
We can also convert the fraction 3/11 into a decimal and then multiply by 100 to find the percentage:
3 ÷ 11 ≈ 0.2727
0.2727 * 100 ≈ 27.27%
This method reinforces the direct relationship between fractions, decimals, and percentages.
Understanding the Approximation
Notice that in all methods, we obtain an approximate value of 27.27%. This is because the fraction 3/11 is a repeating decimal (0.272727...). We typically round to a reasonable number of decimal places for practical purposes. In many contexts, rounding to two decimal places (27.27%) is sufficient.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-world scenarios:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For instance, understanding the percentage change in your investment portfolio over time is crucial for financial planning.
- Retail: Discounts and sales are often expressed as percentages. Calculating the final price after a discount involves percentage calculations. Similarly, sales tax is usually a percentage of the purchase price.
- Science: Percentage calculations are vital in many scientific fields. For example, calculating the percentage of a certain element in a compound, expressing experimental error as a percentage, or determining the percentage change in a population over time all require these skills.
- Data Analysis: Percentages are used extensively in data analysis to represent proportions and trends. For instance, you might express survey results as percentages to show the distribution of opinions.
- Everyday Life: From calculating tips in restaurants to understanding nutritional information on food labels, percentage calculations are integrated into our daily lives.
Expanding the Concept: Finding the Whole or the Part
While we focused on finding the percentage, the same principles can be used to find the whole or the part if the percentage and either the whole or the part are known. Let's illustrate this:
Scenario 1: Finding the Whole
- Problem: 20% of what number is 6?
- Solution: We can set up a proportion: 20/100 = 6/x. Solving for x, we find x = 30. Therefore, 20% of 30 is 6.
Scenario 2: Finding the Part
- Problem: What is 35% of 80?
- Solution: We can use the formula: (35/100) * 80 = 28. Therefore, 35% of 80 is 28.
Advanced Percentage Concepts
For those seeking a deeper understanding, consider these advanced concepts:
- Percentage Increase/Decrease: This involves calculating the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] * 100.
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. It's a fundamental concept in finance.
- Percentage Points: It's important to differentiate between percentage points and percentages. A change from 10% to 15% is a 5 percentage point increase, but a 50% increase in the percentage itself.
Conclusion: Mastering Percentage Calculations
Understanding percentage calculations is a fundamental skill with broad applications. Whether you're dealing with financial matters, scientific data, or everyday problems, the ability to calculate percentages accurately and efficiently will greatly enhance your problem-solving abilities. By mastering the various methods discussed in this article, you'll be well-equipped to tackle a wide range of percentage-related challenges and confidently navigate the numerical world around you. Remember to practice regularly, and you'll soon find these calculations become second nature. The simple problem of "What percent of 11 is 3?" serves as a gateway to a much larger and more versatile understanding of percentages and their practical implications.
Latest Posts
Latest Posts
-
Lowest Common Multiple Of 28 And 24
May 24, 2025
-
How Many Months Are Left In 2024
May 24, 2025
-
30 Minutes From Now What Time Will It Be
May 24, 2025
-
What Is The Gcf Of 100 And 30
May 24, 2025
-
What Is 1 8 Of 32
May 24, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 11 Is 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.