5 6 Divided By 2 3 In Fraction Form
listenit
May 23, 2025 · 5 min read
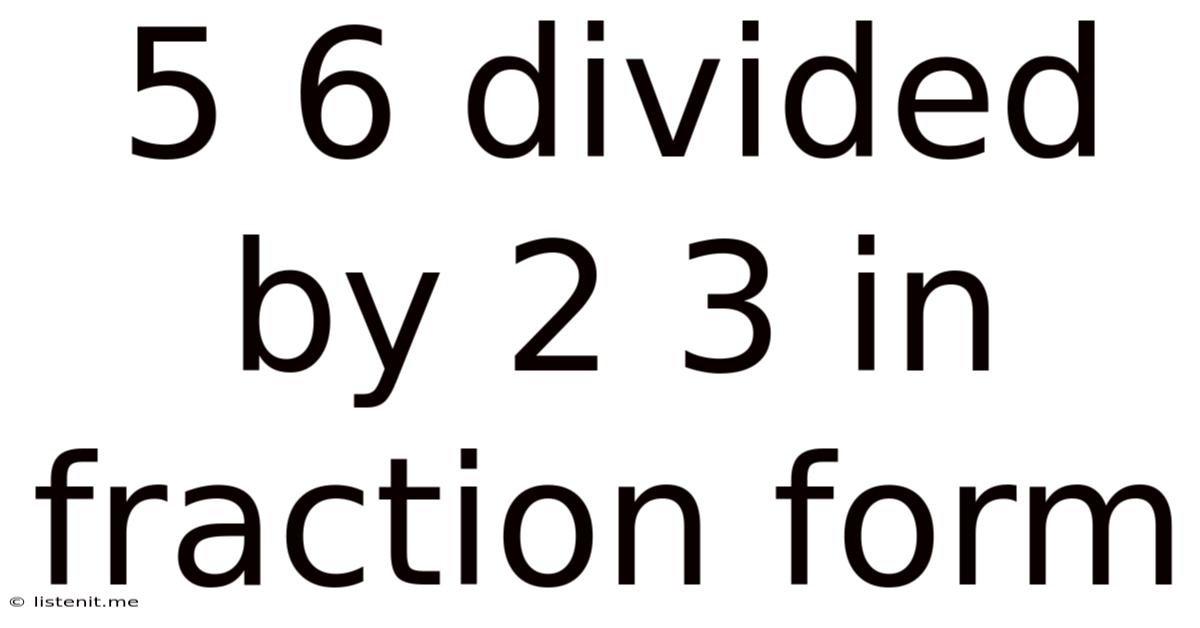
Table of Contents
5/6 Divided by 2/3 in Fraction Form: A Comprehensive Guide
Understanding fraction division can be tricky, but it's a fundamental concept in mathematics with wide-ranging applications. This comprehensive guide will walk you through the process of dividing 5/6 by 2/3, explaining the underlying principles and providing various approaches to solve this problem and similar fraction division problems. We’ll delve into the mechanics, explore different methods, and offer practical examples to solidify your understanding.
Understanding Fraction Division
Before we tackle the specific problem of 5/6 ÷ 2/3, let's review the basics of dividing fractions. The core principle is to flip the second fraction (the divisor) and multiply. This process is also known as multiplying by the reciprocal.
What is a Reciprocal?
The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2. The reciprocal of a whole number can be found by putting it over 1; the reciprocal of 5 is 1/5.
Why Does Flipping and Multiplying Work?
The reason this method works stems from the definition of division. Dividing by a fraction is the same as multiplying by its reciprocal. Consider this: dividing by 2 is the same as multiplying by 1/2. This same logic extends to all fractions.
Calculating 5/6 Divided by 2/3
Now, let's apply this knowledge to our problem: 5/6 ÷ 2/3.
Step 1: Find the reciprocal of the second fraction.
The reciprocal of 2/3 is 3/2.
Step 2: Change the division sign to a multiplication sign.
Our problem now becomes: 5/6 × 3/2.
Step 3: Multiply the numerators (top numbers) together.
5 × 3 = 15
Step 4: Multiply the denominators (bottom numbers) together.
6 × 2 = 12
Step 5: Simplify the resulting fraction.
Our answer is 15/12. However, this fraction can be simplified. Both the numerator and denominator are divisible by 3:
15 ÷ 3 = 5 12 ÷ 3 = 4
Therefore, the simplified answer is 5/4. This can also be expressed as a mixed number: 1 ¼.
Alternative Methods for Fraction Division
While the "flip and multiply" method is the most common and efficient, there are other ways to approach fraction division problems. Let's explore a couple of them:
Method 2: Using Common Denominators
This method involves finding a common denominator for both fractions before dividing. While it's generally less efficient than the "flip and multiply" method, it can be helpful for building a deeper understanding of fraction division.
Step 1: Find a common denominator.
For 5/6 and 2/3, the least common denominator (LCD) is 6.
Step 2: Convert the fractions to have the common denominator.
5/6 already has the denominator 6. To convert 2/3, we multiply both the numerator and denominator by 2: 2/3 × 2/2 = 4/6.
Step 3: Divide the numerators.
Now we have 5/6 ÷ 4/6. We can divide the numerators directly: 5 ÷ 4 = 1 ¼ or 5/4.
Method 3: Converting to Decimal Numbers (Approximation)
This method involves converting the fractions to decimal numbers before dividing. This approach is useful for estimations or when dealing with more complex fractions. However, it will only offer an approximate result because you might lose some precision during the conversion.
Step 1: Convert the fractions to decimals.
5/6 ≈ 0.833 2/3 ≈ 0.667
Step 2: Divide the decimal numbers.
0.833 ÷ 0.667 ≈ 1.249
This result is an approximation of 5/4 (1.25). Keep in mind that using decimals can introduce rounding errors, making this method less precise than the other methods explained.
Practical Applications of Fraction Division
Fraction division isn't just a theoretical exercise; it's a crucial skill with many real-world applications. Here are a few examples:
-
Cooking and Baking: Recipes often require dividing ingredients into fractions. For example, if a recipe calls for 2/3 cup of flour and you only want to make half the recipe, you'll need to divide 2/3 by 2.
-
Sewing and Crafting: Many crafting projects involve precise measurements, often expressed in fractions of an inch or centimeter. Dividing these measurements is essential for accurate work.
-
Construction and Engineering: Engineers and builders frequently work with fractional measurements and ratios. Dividing fractions accurately is critical for structural integrity and project success.
-
Finance and Budgeting: Dividing your budget into fractional portions to allocate spending is a practical application of fraction division.
-
Data Analysis: Working with datasets often involves handling fractional values, requiring division operations to calculate rates, proportions, or ratios.
Addressing Potential Challenges and Common Mistakes
While the "flip and multiply" method is straightforward, some common mistakes can occur:
-
Forgetting to find the reciprocal: Remember to flip the second fraction before multiplying.
-
Incorrect multiplication: Carefully multiply the numerators and denominators.
-
Failure to simplify: Always simplify the resulting fraction to its lowest terms.
-
Mixing up operations: Remember to follow the order of operations (PEMDAS/BODMAS) when dealing with multiple operations in a single problem.
Conclusion: Mastering Fraction Division
Mastering fraction division is a valuable skill that opens doors to more advanced mathematical concepts. The "flip and multiply" method, coupled with a clear understanding of reciprocals, provides the most efficient approach. Remember to practice regularly and thoroughly check your work, paying close attention to the simplification process. Through consistent practice and the application of these methods, you can confidently tackle any fraction division problem, including 5/6 divided by 2/3. This ability will not only enhance your mathematical proficiency but also equip you with essential problem-solving skills applicable to various real-world scenarios. Remember to always double-check your work and explore different methods to find what works best for you!
Latest Posts
Latest Posts
-
What Is 7 5 In A Fraction
May 24, 2025
-
1 X 1 X 1 4
May 24, 2025
-
What Is 40 Off Of 70 Dollars
May 24, 2025
-
What Is 28 Days From Todays Date
May 24, 2025
-
1958 Was How Many Years Ago
May 24, 2025
Related Post
Thank you for visiting our website which covers about 5 6 Divided By 2 3 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.