1 X 1 X 1 4
listenit
May 24, 2025 · 7 min read
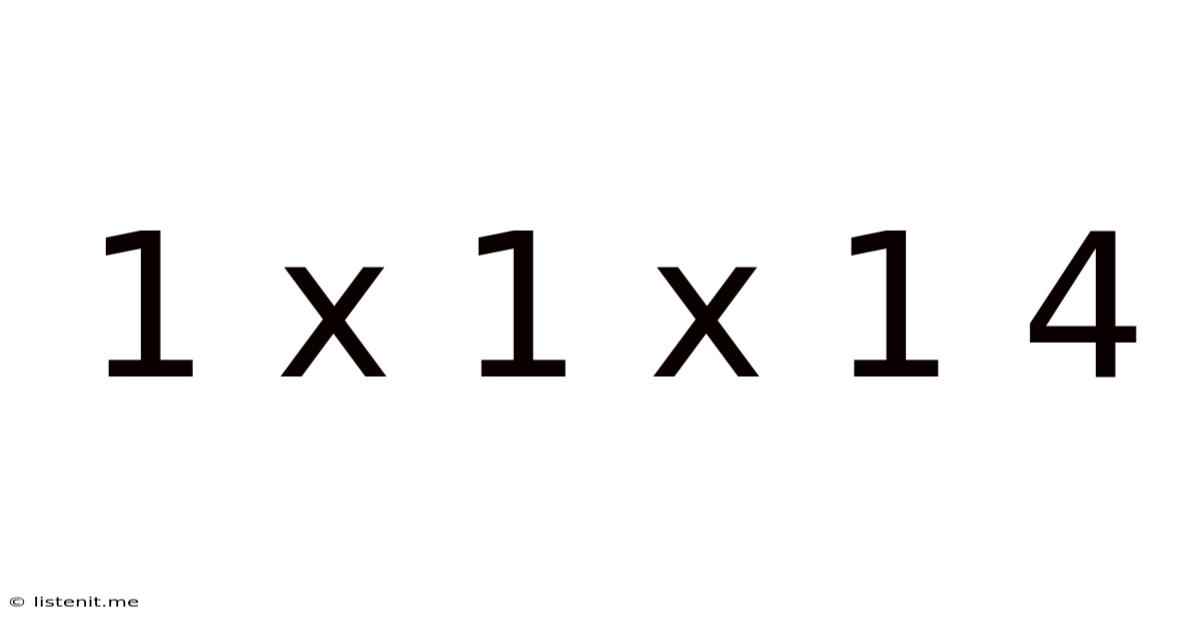
Table of Contents
1 x 1 x 1 = 4: Exploring the Illusions of Mathematical Truth
The seemingly simple equation, 1 x 1 x 1 = 4, immediately strikes us as false. Basic arithmetic dictates that the product of one multiplied by itself three times is, unequivocally, one. Yet, the very existence of this statement, presented as a puzzle or a paradox, hints at deeper concepts within mathematics, logic, and even the nature of truth itself. This exploration delves into the ways in which such a seemingly absurd equation can be "proven" and the valuable lessons it teaches about critical thinking, the limitations of mathematical axioms, and the seductive power of flawed logic.
The Allure of the Impossible: Why We're Drawn to 1 x 1 x 1 = 4
The appeal of this "mathematical fallacy" lies in its inherent contradiction. It challenges our fundamental understanding of arithmetic, forcing us to question our assumptions and engage in critical analysis. This inherent challenge activates a natural curiosity, prompting us to seek out the "trick" or the hidden manipulation. This inherent curiosity is a powerful tool in learning; it pushes us to actively engage with the material and not simply passively accept it. The inherent 'wrongness' also serves as a powerful learning tool, by demonstrating that there's always more to be explored than what initially seems true.
The Psychology of Mathematical Puzzles
Our brains are wired to seek patterns and solve problems. Mathematical puzzles, particularly those that appear paradoxical, tap into this inherent drive. The satisfaction of uncovering the deception, the "aha!" moment of understanding, reinforces this behavior and encourages further exploration of mathematical concepts. The equation "1 x 1 x 1 = 4" acts as a cognitive puzzle, engaging our problem-solving skills and rewarding us with a deeper understanding of mathematical reasoning.
Deconstructing the Illusion: Unveiling the Methods
The "proofs" of 1 x 1 x 1 = 4 typically rely on subtle mathematical manipulations, often involving hidden divisions by zero, incorrect algebraic operations, or cleverly disguised errors in notation. These "proofs" highlight the importance of paying close attention to detail and meticulously checking each step in a mathematical argument. Let's examine some common approaches and expose their fallacies:
Method 1: The Misleading Manipulation of Square Roots
One common "proof" involves the manipulation of square roots. It might begin with a seemingly legitimate equation and then proceed with steps that appear correct but ultimately conceal a violation of mathematical rules. For example, a flawed "proof" might involve manipulating the equation (x-1)² = 0 and arriving at the erroneous conclusion that x=1 and x= -2, leading to an incorrect chain of arguments that ends up with 1 x 1 x 1 = 4.
The Fallacy: The problem lies in the unjustified manipulation of the equation, often involving incorrect square root operations or neglecting to consider all possible solutions. In many cases, dividing by zero or similar errors are cleverly hidden within seemingly simple algebraic steps.
Method 2: The Hidden Division by Zero
Another common tactic involves cleverly concealing a division by zero, a mathematical operation that is undefined and leads to nonsensical results. The "proof" might use a series of algebraic manipulations to create a situation where the division by zero is masked, leading to a spurious outcome like 1 x 1 x 1 = 4.
The Fallacy: Division by zero is a fundamental error in mathematics. Any "proof" that relies on this operation is invalid. The key to spotting this fallacy is to carefully examine each step in the argument to ensure that no division by zero is taking place.
Method 3: The Trickery of Improper Notation
Some "proofs" rely on ambiguous or misleading notation to obfuscate the logical errors. For example, they might manipulate symbols or use unconventional notations to create an illusion of correctness. These 'proofs' often appear convincing to those unfamiliar with formal mathematical notation and rules.
The Fallacy: Mathematical notation has precise rules and conventions. Any deviation from these rules can lead to ambiguity and invalid results. Understanding standard mathematical notation and its conventions is vital in assessing the validity of mathematical arguments.
The Educational Value of Mathematical Fallacies
Despite their deceptive nature, these mathematical paradoxes serve a valuable pedagogical purpose. They encourage students to think critically about mathematical processes and to carefully examine every step in a mathematical argument. By exposing the errors in these fallacious "proofs," students gain a deeper understanding of the underlying principles of mathematics and improve their ability to distinguish between valid and invalid arguments.
Strengthening Critical Thinking Skills
Encountering and dissecting fallacies helps students develop critical thinking skills that extend beyond mathematics. The ability to identify logical flaws, examine assumptions, and evaluate evidence is crucial in all aspects of life, from evaluating scientific claims to making informed decisions. The experience of being initially misled by a mathematical fallacy encourages a more meticulous and cautious approach to all forms of reasoning.
Improving Problem-Solving Abilities
The challenge posed by these "proofs" sharpens problem-solving skills. Students are forced to analyze complex steps, identify the subtle errors, and reconstruct the logic to uncover the deception. This process enhances their ability to systematically approach problems, develop strategies for finding solutions, and systematically evaluate their results.
Enhancing Mathematical Intuition
While mathematical rigor and precision are crucial, intuition also plays a vital role in mathematical understanding. These fallacies encourage students to develop their mathematical intuition by comparing the results of an argument to their intuitive understanding of the concept being studied. If the result conflicts with their intuition, it serves as a signal to further investigate the argument for underlying errors.
Beyond the Numbers: Metaphorical Interpretations
The seemingly absurd equation 1 x 1 x 1 = 4 can also be interpreted metaphorically, prompting reflections on wider aspects of life and understanding. It can be a representation of the subjective nature of truth or the possibility of multiple perspectives. The equation, while mathematically incorrect, can symbolize how a seemingly impossible outcome might appear true depending on the context or the lens through which we view it.
The Subjectivity of Truth
In a broader sense, the equation can symbolize the subjective nature of truth. What may appear as an indisputable fact in one context might be perceived differently in another. The "proofs" that attempt to establish 1 x 1 x 1 = 4 rely on manipulating established rules or introducing assumptions that are not inherently true. This can be seen as a reflection of how different perspectives and interpretations can shape our understanding of reality.
The Power of Perspective
The fallacy also highlights the significance of perspective. Depending on the assumptions made or the methods employed, even an incorrect conclusion can appear convincing. This resonates with many aspects of life, emphasizing that our interpretations and conclusions are always influenced by our perspectives and biases.
The Importance of Context
The context in which an argument is presented greatly affects its interpretation. A statement like "1 x 1 x 1 = 4" might be interpreted differently depending on whether it's presented as a mathematical problem, a philosophical puzzle, or a rhetorical device. Understanding the context is essential for proper interpretation and critical evaluation.
Conclusion: Embracing the Illusions
The equation "1 x 1 x 1 = 4," while demonstrably false in conventional mathematics, serves as a valuable tool for exploring the intricacies of mathematical reasoning, the power of critical thinking, and even the subjective nature of truth. By analyzing its deceptive "proofs," we develop sharper problem-solving skills, enhance our mathematical intuition, and gain a deeper appreciation for the importance of rigorous methodology in all areas of inquiry. The seemingly absurd equation ultimately becomes a testament to the power of critical thinking and the continuous need to question, analyze, and refine our understanding of the world around us, both mathematical and otherwise. Its enduring appeal lies in its ability to both challenge and educate, reminding us that the pursuit of truth often involves navigating through illusion and ambiguity.
Latest Posts
Latest Posts
-
How To Calculate Z Score On Calculator
May 24, 2025
-
3 Is 1 Of What Amount
May 24, 2025
-
400 Sq In To Sq Ft
May 24, 2025
-
What Is 20 Of 10 Dollars
May 24, 2025
-
1 3 5 6 1 X
May 24, 2025
Related Post
Thank you for visiting our website which covers about 1 X 1 X 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.