5 17 Squared 10 Third Power
listenit
May 24, 2025 · 4 min read
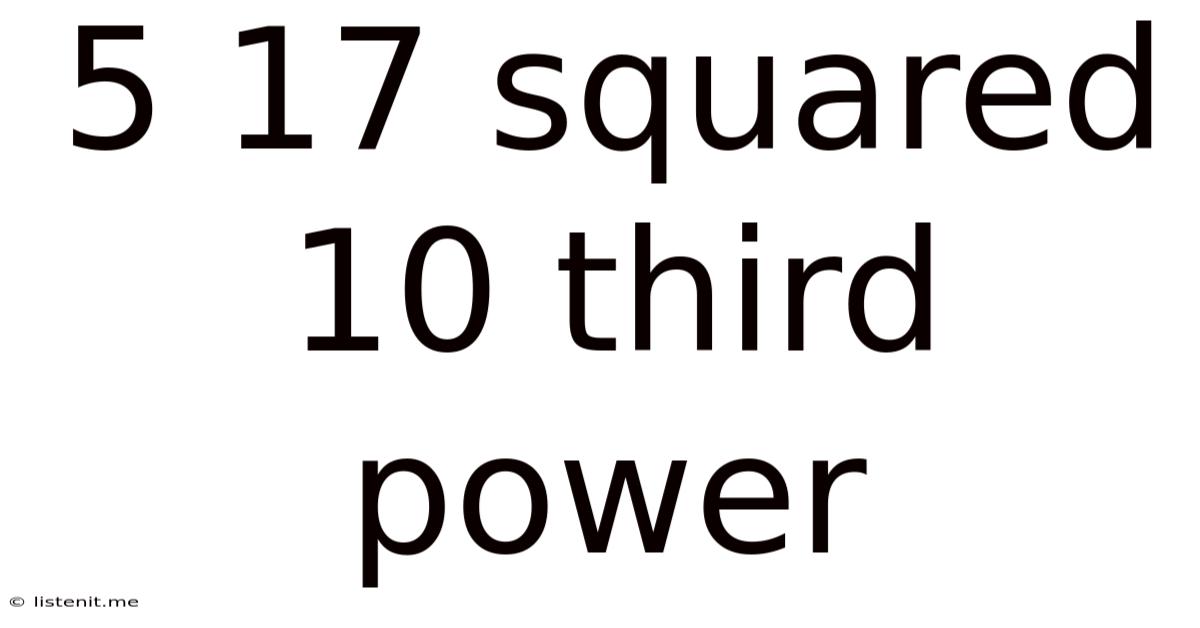
Table of Contents
Decoding the Mathematical Puzzle: 5, 17 Squared, 10 Cubed
This article delves into the intriguing mathematical puzzle presented by the sequence: 5, 17 squared, 10 cubed. We'll explore the individual components, their calculations, and then examine potential relationships or patterns within the sequence. Understanding this seemingly simple sequence offers a glimpse into fundamental mathematical concepts and opens doors to more complex explorations.
Understanding the Basics: Squares and Cubes
Before diving into the specifics of 5, 17 squared, and 10 cubed, let's refresh our understanding of squares and cubes.
Squares: A square of a number is the result of multiplying that number by itself. For instance, the square of 5 (written as 5²) is 5 x 5 = 25. It's essentially raising the number to the power of 2.
Cubes: A cube of a number is the result of multiplying the number by itself three times. For example, the cube of 10 (written as 10³) is 10 x 10 x 10 = 1000. This represents raising the number to the power of 3.
Calculating the Sequence: 5, 17², 10³
Now, let's calculate each element of our sequence:
-
5: This is a straightforward integer; no calculation is needed.
-
17² (17 squared): 17 x 17 = 289. This is the result of squaring the number 17.
-
10³ (10 cubed): 10 x 10 x 10 = 1000. This is the result of cubing the number 10.
Therefore, our complete sequence, with the calculations performed, is: 5, 289, 1000.
Exploring Potential Relationships and Patterns
The sequence 5, 289, 1000 doesn't immediately reveal an obvious arithmetic or geometric progression. There's no constant difference or ratio between consecutive terms. However, we can explore various mathematical avenues to search for hidden relationships.
1. Differences between terms:
Let's examine the differences between consecutive terms:
- 289 - 5 = 284
- 1000 - 289 = 711
The differences themselves don't show a clear pattern.
2. Ratios between terms:
Let's look at the ratios between consecutive terms:
- 289 / 5 ≈ 57.8
- 1000 / 289 ≈ 3.46
Again, no readily apparent pattern emerges from the ratios.
3. Considering the Prime Factorization:
A deeper analysis might involve considering the prime factorization of each number:
- 5: 5 (already a prime number)
- 289: 17 x 17 (17²)
- 1000: 2 x 2 x 2 x 5 x 5 x 5 (2³ x 5³)
While the prime factorization reveals the fundamental building blocks of each number, it doesn't immediately point to a unifying pattern within the sequence.
4. Exploring Polynomial Relationships:
It's possible that the sequence could be generated by a polynomial function. However, determining such a function requires more terms in the sequence. With only three terms, it's difficult to definitively establish a polynomial relationship.
5. Geometric Interpretation:
While not immediately apparent, a geometric interpretation might exist. Perhaps these numbers represent specific dimensions or areas in a geometric problem. However, without further context or information, this remains speculative.
Expanding the Possibilities: Adding Context
The nature of mathematical puzzles often lies in their context. The sequence "5, 17 squared, 10 cubed" is quite abstract without additional information. Its meaning and potential relationships could drastically change depending on the context:
- A physics problem: The numbers could represent quantities like mass, velocity, or time.
- A coding sequence: The numbers might be used as parameters or indices in a program.
- A geometrical problem: The numbers could correspond to lengths, areas, or volumes.
- A number theory puzzle: The sequence might be part of a larger pattern involving prime numbers, perfect squares, or other number-theoretic properties.
Without knowing the context or the origin of this sequence, finding a meaningful relationship remains challenging. The focus should be on exploring various mathematical techniques to understand the inherent properties of each number and look for potential connections.
Advanced Mathematical Explorations:
For those with a more advanced mathematical background, investigating the sequence could involve more complex tools and concepts. For example:
- Continued fractions: Representing the numbers as continued fractions might reveal patterns not visible in their decimal representation.
- Modular arithmetic: Exploring the properties of these numbers modulo different integers could unveil hidden structures.
- Number theory functions: Investigating how these numbers behave under various number theory functions (like Euler's totient function) might uncover relationships.
Conclusion: The Importance of Context and Exploration
The sequence 5, 17 squared, 10 cubed presents a fascinating mathematical puzzle. While a simple, readily apparent relationship isn't immediately obvious, the exploration process itself is valuable. It underscores the importance of:
- Fundamental mathematical concepts: Understanding squares, cubes, prime factorization, and other basic mathematical tools is crucial for tackling such problems.
- Systematic investigation: A methodical approach, exploring differences, ratios, prime factorization, and potential polynomial relationships, is essential.
- Contextual understanding: The meaning and significance of a mathematical sequence often depend heavily on its context. Without further information, the possibilities remain open-ended.
Ultimately, the value of this puzzle extends beyond finding a definitive solution. It encourages critical thinking, problem-solving skills, and a deeper appreciation for the interconnectedness of mathematical concepts. The journey of exploration, rather than just the destination, holds significant educational value. The more we explore, the more we understand the beauty and complexity of mathematics. This exploration serves as a microcosm of the larger mathematical landscape, emphasizing the importance of persistent inquiry and creative thinking in unraveling numerical mysteries.
Latest Posts
Latest Posts
-
1 Of 15 Is What Percent
May 24, 2025
-
Greatest Common Factor Of 52 And 68
May 24, 2025
-
5 17 2 10 To The 3rd Power
May 24, 2025
-
What Is The Least Common Multiple Of 20 And 5
May 24, 2025
-
What Is The Prime Factorization Of 250
May 24, 2025
Related Post
Thank you for visiting our website which covers about 5 17 Squared 10 Third Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.