490 Out Of 700 As A Percentage
listenit
May 24, 2025 · 5 min read
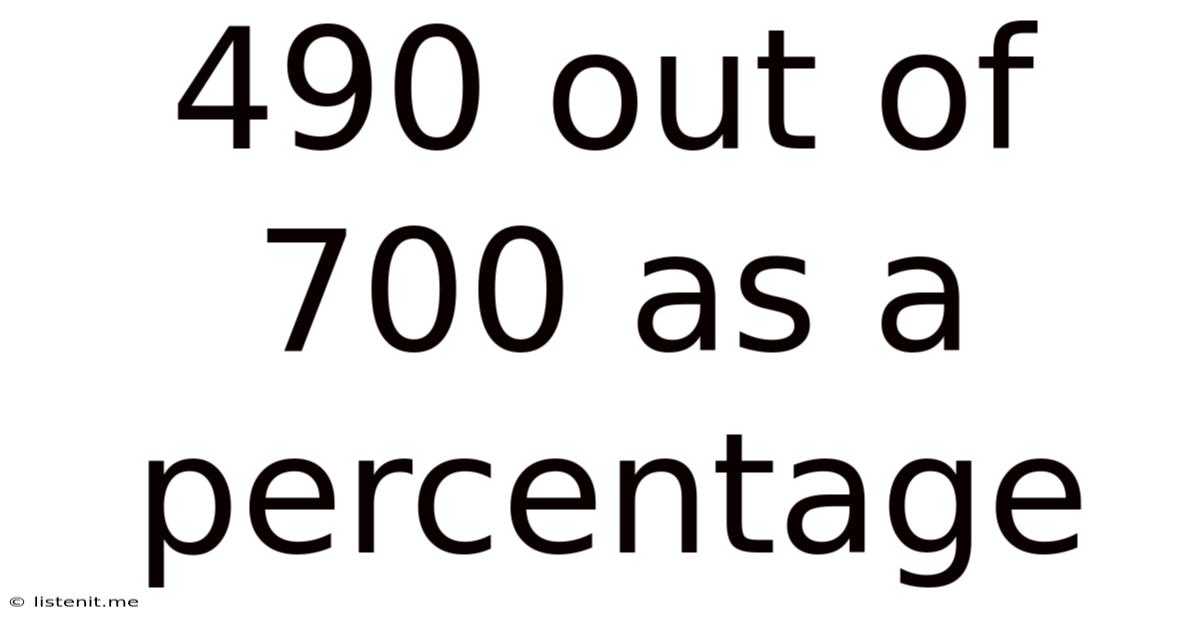
Table of Contents
490 out of 700 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday finances to complex statistical analyses. This comprehensive guide delves into the specifics of calculating "490 out of 700 as a percentage," providing a step-by-step approach and exploring related concepts to solidify your understanding.
Understanding Percentages
Before we dive into the calculation, let's establish a firm grasp of what a percentage represents. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "per hundred." For instance, 50% signifies 50 out of 100, which is equivalent to 50/100 or 1/2. Understanding this basic concept is crucial for all percentage calculations.
Calculating 490 out of 700 as a Percentage: The Step-by-Step Approach
Calculating "490 out of 700 as a percentage" involves a straightforward process:
-
Express the Numbers as a Fraction: The first step is to express the given values as a fraction. In this case, the fraction becomes 490/700. This represents the part (490) over the whole (700).
-
Convert the Fraction to a Decimal: To convert the fraction to a decimal, we divide the numerator (490) by the denominator (700): 490 ÷ 700 = 0.7
-
Convert the Decimal to a Percentage: To express the decimal as a percentage, we multiply it by 100 and add the "%" symbol: 0.7 x 100 = 70%.
Therefore, 490 out of 700 is 70%.
Alternative Calculation Methods
While the above method is the most straightforward, other methods can achieve the same result. These alternative approaches offer flexibility depending on your preference and the complexity of the calculation.
Method 2: Simplifying the Fraction First
Before converting to a decimal, we can simplify the fraction 490/700 by finding the greatest common divisor (GCD). The GCD of 490 and 700 is 70. Dividing both the numerator and the denominator by 70 simplifies the fraction:
490 ÷ 70 = 7 700 ÷ 70 = 10
This simplifies the fraction to 7/10. Converting 7/10 to a decimal (7 ÷ 10 = 0.7) and then to a percentage (0.7 x 100 = 70%) yields the same result: 70%. This method is particularly useful when dealing with larger numbers that might be cumbersome to directly divide.
Method 3: Using Proportions
The problem can also be solved using proportions. We set up a proportion:
490/700 = x/100
Here, 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
700x = 49000
Then, divide both sides by 700:
x = 49000/700 = 70
Therefore, x = 70%, confirming our previous calculations. This method is valuable when dealing with problems involving finding a percentage of a given quantity or when working with proportions in different contexts.
Practical Applications of Percentage Calculations
The ability to calculate percentages is a vital skill with countless real-world applications. Here are some examples:
-
Finance: Calculating interest rates, discounts, tax percentages, profit margins, and investment returns. Understanding percentage changes is essential for tracking financial performance.
-
Statistics: Percentages are used extensively in statistical analysis to represent proportions, frequencies, and probabilities. They're critical in data interpretation and drawing conclusions from surveys and studies.
-
Education: Calculating grades, test scores, and performance metrics. Understanding percentages is crucial for assessing student progress and identifying areas for improvement.
-
Science: Percentages are used to express concentrations of solutions, error rates in experiments, and changes in physical quantities.
-
Everyday Life: Calculating tips in restaurants, determining sale discounts in shops, understanding nutritional information on food labels, and comprehending various statistics in news reports.
Advanced Percentage Calculations: Beyond the Basics
While calculating "490 out of 700 as a percentage" is a relatively simple calculation, it provides a foundation for more complex percentage problems. Let's explore some of these advanced concepts:
Calculating Percentage Increase or Decrease
Percentage increase or decrease calculations are frequently encountered when analyzing changes over time. The formula is:
[(New Value - Old Value) / Old Value] x 100%
For example, if a value increases from 500 to 600, the percentage increase is:
[(600 - 500) / 500] x 100% = 20%
Similarly, if a value decreases from 600 to 500, the percentage decrease is:
[(500 - 600) / 600] x 100% = -16.67%
Finding the Original Value after a Percentage Change
Sometimes, you might know the final value and the percentage change and need to find the original value. This requires rearranging the percentage change formula.
Calculating Percentage Points
It's important to differentiate between percentage change and percentage points. A percentage point represents the absolute difference between two percentages, while a percentage change represents the relative difference. For instance, if interest rates increase from 5% to 8%, the increase is 3 percentage points, but the percentage increase is 60% [(8-5)/5 * 100%]. This distinction is crucial for accurate interpretation and communication of data.
Troubleshooting Common Percentage Calculation Mistakes
Several common errors can occur when calculating percentages:
- Incorrect Order of Operations: Always follow the order of operations (PEMDAS/BODMAS) to avoid errors.
- Mixing up Percentage and Percentage Points: Clearly understand the difference and use the appropriate calculation method.
- Using the Wrong Formula: Choose the appropriate formula based on the specific problem you're solving.
- Rounding Errors: Be mindful of rounding errors, particularly when performing multiple calculations. Keep as many decimal places as possible during intermediate steps and round only the final answer.
Conclusion: Mastering Percentage Calculations for Success
Mastering percentage calculations is a valuable skill that transcends various academic and professional fields. From simple calculations like "490 out of 700 as a percentage" to more advanced applications, a strong understanding of percentage calculations empowers you to interpret data, make informed decisions, and succeed in various aspects of life. By employing the step-by-step approach, exploring alternative methods, and understanding the practical applications and potential pitfalls, you can confidently tackle percentage calculations and utilize them effectively. Remember to practice regularly to strengthen your skills and build confidence in this essential mathematical skill.
Latest Posts
Latest Posts
-
Highest Common Factor Of 3 And 6
May 25, 2025
-
Write Quadratic Equation With Given Roots Calculator
May 25, 2025
-
How To Figure Out Square Footage For Tile
May 25, 2025
-
14 To The Power Of 4
May 25, 2025
-
How Many Months Ago Was Christmas 2023
May 25, 2025
Related Post
Thank you for visiting our website which covers about 490 Out Of 700 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.