41.5 Out Of 50 As A Percentage
listenit
May 25, 2025 · 4 min read
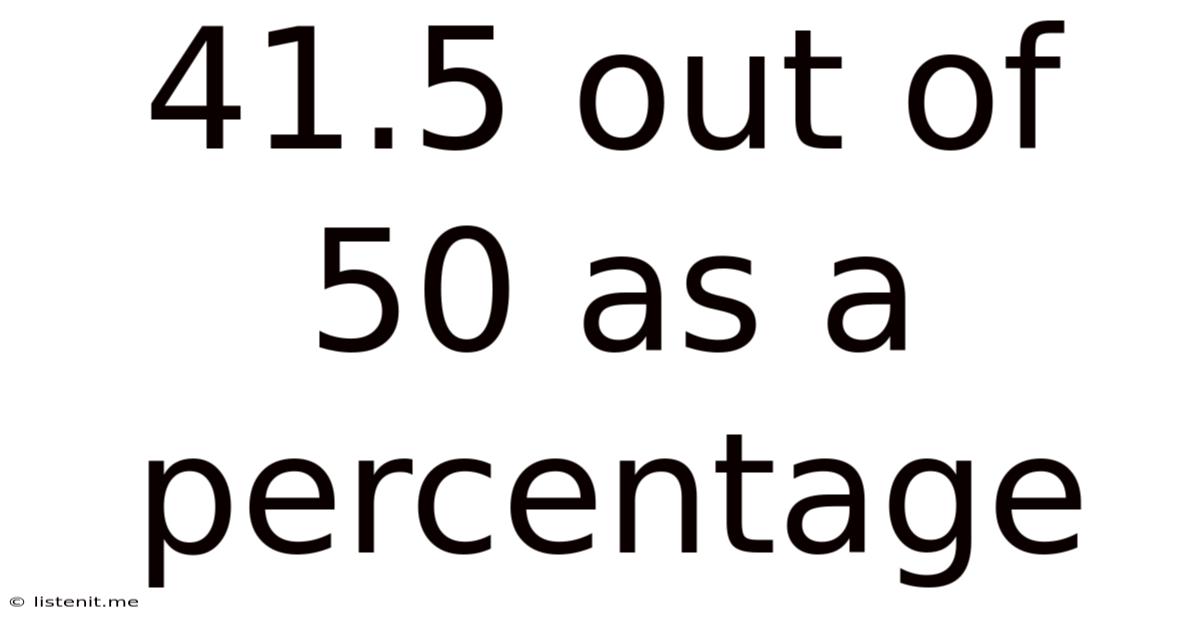
Table of Contents
41.5 out of 50 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from academic assessments to financial analyses. Understanding how to convert fractions and decimals into percentages is crucial for interpreting data accurately and making informed decisions. This comprehensive guide delves into the calculation of 41.5 out of 50 as a percentage, providing a step-by-step explanation, exploring variations and applications, and offering valuable insights into percentage calculations in general.
Understanding Percentages
A percentage represents a fraction of 100. The term "percent" literally means "per hundred." Therefore, a percentage expresses a proportion relative to a whole, which is considered 100%. For instance, 50% signifies 50 out of 100, or half of the total.
Calculating 41.5 out of 50 as a Percentage
To determine the percentage representation of 41.5 out of 50, we follow these simple steps:
Step 1: Formulate the Fraction
First, express the given values as a fraction: 41.5/50
Step 2: Convert the Fraction to a Decimal
Divide the numerator (41.5) by the denominator (50):
41.5 ÷ 50 = 0.83
Step 3: Convert the Decimal to a Percentage
Multiply the decimal by 100 and add the percentage sign (%):
0.83 × 100 = 83%
Therefore, 41.5 out of 50 is 83%.
Alternative Calculation Methods
While the above method is straightforward, alternative approaches can be used, depending on the context and individual preference.
Method 1: Using Proportions
We can set up a proportion to solve for the percentage:
41.5/50 = x/100
Cross-multiplying, we get:
50x = 4150
Solving for x:
x = 4150/50 = 83
Therefore, x = 83%, confirming our previous calculation.
Method 2: Using Percentage Formula Directly
The fundamental percentage formula is:
(Part / Whole) * 100% = Percentage
Substituting our values:
(41.5 / 50) * 100% = 83%
This method directly applies the core concept of percentages, highlighting the relationship between the part (41.5), the whole (50), and the resulting percentage.
Real-world Applications of Percentage Calculations
Understanding percentage calculations is vital in various real-world scenarios:
-
Academic Performance: Calculating grades based on scores obtained in exams or assignments. For example, a score of 41.5 out of 50 in a test represents a strong 83% performance.
-
Financial Analysis: Determining interest rates, calculating discounts, analyzing investment returns, and understanding profit margins all rely heavily on percentage calculations. A business might analyze sales data, where 41.5 units sold out of a possible 50 represents an 83% sales conversion rate.
-
Data Interpretation: Analyzing survey results, statistical data, and scientific findings often involves interpreting percentages to understand trends and draw meaningful conclusions. For example, if a survey shows 41.5 out of 50 respondents prefer a specific product, this translates to an 83% preference rate.
-
Sales and Marketing: Calculating discounts, understanding market share, and tracking conversion rates all utilize percentage calculations. This 83% figure could represent a strong customer preference, which is crucial for marketing decisions.
Handling Different Scenarios
While 41.5 out of 50 is a relatively straightforward calculation, let's explore how to handle variations:
-
Decimals in the Whole: If the total value (whole) also contains a decimal, the calculation remains the same. For example, 41.5 out of 50.5 would be calculated as (41.5 / 50.5) * 100%.
-
Larger Numbers: The principle remains the same regardless of the magnitude of the numbers involved. The calculation method is consistent whether we are dealing with small numbers or large datasets.
-
Rounding: Depending on the context, rounding the final percentage may be necessary. For example, you might round 83.00% to 83%.
-
Percentages Greater than 100%: In situations where the part exceeds the whole, the resulting percentage will be greater than 100%. This often occurs in scenarios involving growth or increase.
Advanced Percentage Calculations
Beyond the basic calculations, understanding more advanced concepts is beneficial for a comprehensive grasp of percentages:
-
Percentage Change: This measures the relative change between two values. It's calculated as [(New Value - Old Value) / Old Value] * 100%.
-
Percentage Point Change: This refers to the absolute difference between two percentages. It's simply the difference between the two percentages. It's crucial to distinguish between percentage change and percentage point change.
-
Compounding Percentages: This involves calculating percentages sequentially, where the result of one percentage calculation becomes the base for the next. This is frequently used in finance, especially with compound interest calculations.
Importance of Accuracy in Percentage Calculations
Accuracy in percentage calculations is paramount. Inaccurate calculations can lead to incorrect interpretations, flawed decisions, and potentially significant financial repercussions. Always double-check your work and utilize appropriate tools or calculators to ensure precise results. Paying attention to detail and understanding the context of the problem are vital for avoiding errors.
Conclusion
Calculating 41.5 out of 50 as a percentage yields 83%, a straightforward but fundamental calculation with wide-ranging applications. Mastering percentage calculations empowers you to interpret data accurately, make informed decisions, and effectively communicate quantitative information across various disciplines. Understanding the underlying principles and different calculation methods will equip you to confidently handle a variety of percentage-related problems, both simple and complex. By understanding percentages, you unlock a vital key to interpreting data, making decisions, and navigating the quantitative world. Remember to always double-check your work and consider the context of the calculation to ensure accuracy and meaningful results.
Latest Posts
Latest Posts
-
1 5 9 As An Improper Fraction
May 25, 2025
-
11 Out Of 25 As A Percent
May 25, 2025
-
What Is 3 Divided By 6
May 25, 2025
-
4 Divided By 12 In Fraction
May 25, 2025
-
26 2 Miles In 3 Hours Pace
May 25, 2025
Related Post
Thank you for visiting our website which covers about 41.5 Out Of 50 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.