11 Out Of 25 As A Percent
listenit
May 25, 2025 · 5 min read
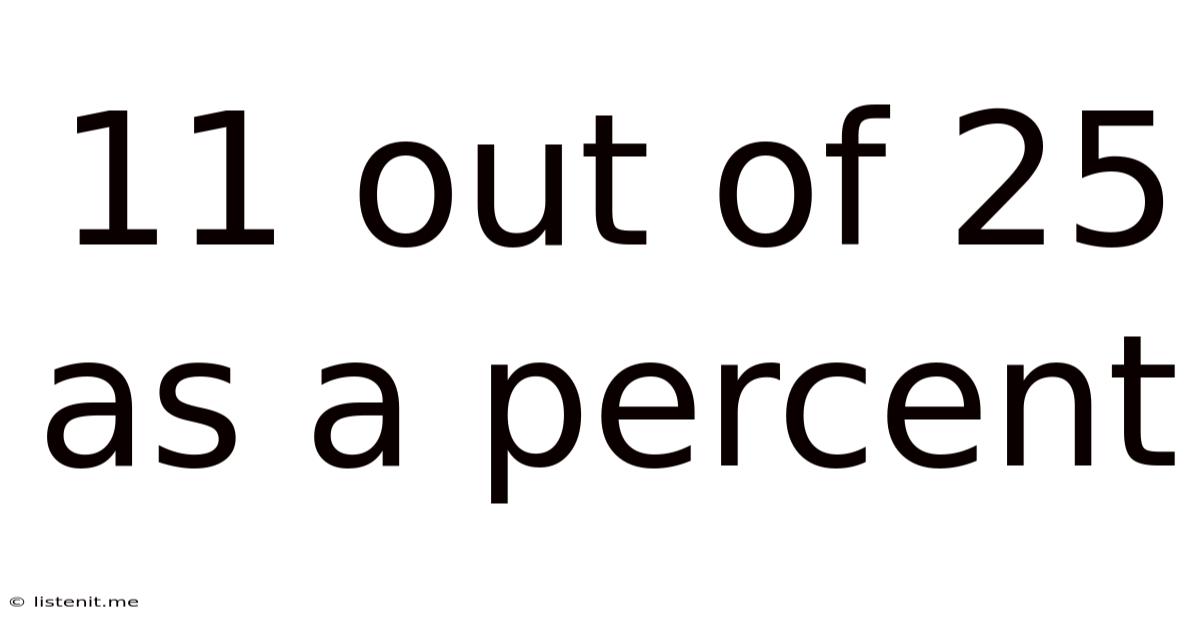
Table of Contents
11 Out of 25 as a Percent: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday finances to complex scientific analyses. Understanding how to convert fractions to percentages is crucial for anyone seeking to master numerical literacy. This comprehensive guide dives deep into the calculation of "11 out of 25 as a percent," explaining the process step-by-step and expanding upon the broader concepts of percentage calculation. We'll explore different methods, address common misconceptions, and offer practical examples to solidify your understanding.
Understanding Percentages
Before we tackle the specific problem of converting "11 out of 25" into a percentage, let's establish a strong foundation. A percentage is simply a fraction where the denominator is 100. It represents a portion or proportion of a whole. The percent symbol (%) is used to denote a percentage.
For example, 50% means 50 out of 100, which can be simplified to 1/2 or 0.5 as a decimal. Understanding this fundamental relationship between fractions, decimals, and percentages is key to mastering percentage calculations.
Method 1: Using the Fraction Method
The most straightforward way to calculate "11 out of 25" as a percentage is to treat it as a fraction and then convert it to a percentage.
Step 1: Express as a Fraction
The phrase "11 out of 25" directly translates to the fraction 11/25.
Step 2: Convert the Fraction to a Decimal
To convert a fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number):
11 ÷ 25 = 0.44
Step 3: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the percent symbol (%):
0.44 x 100 = 44%
Therefore, 11 out of 25 is equal to 44%.
Method 2: Using Proportions
This method involves setting up a proportion to solve for the unknown percentage.
Step 1: Set up the Proportion
We can set up a proportion like this:
11/25 = x/100
Where 'x' represents the percentage we want to find.
Step 2: Cross-Multiply
Cross-multiplying the proportion gives us:
25x = 1100
Step 3: Solve for x
Divide both sides of the equation by 25:
x = 1100 ÷ 25 = 44
Therefore, x = 44%, confirming our result from the previous method.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the process. Simply enter 11 ÷ 25 and then multiply the result by 100. The calculator will automatically display the answer as 44%. This method is particularly useful for more complex calculations.
Practical Applications of Percentage Calculations
Understanding percentage calculations has numerous real-world applications:
- Finance: Calculating interest rates, discounts, taxes, and profit margins. For example, a 44% discount on a $100 item would save you $44.
- Statistics: Representing data in charts and graphs, interpreting survey results, and analyzing probabilities.
- Science: Expressing experimental results, calculating concentrations, and representing data in scientific reports.
- Everyday Life: Calculating tips in restaurants, understanding sales, and comparing prices.
Common Mistakes to Avoid
While percentage calculations are relatively straightforward, there are some common mistakes to watch out for:
- Incorrectly Converting Decimals to Percentages: Remember to multiply the decimal by 100, not just move the decimal point.
- Confusing Percentages with Decimal Values: A percentage is a specific type of fraction (out of 100), while a decimal is a representation of a number less than one.
- Rounding Errors: When dealing with complex calculations involving multiple percentages, pay attention to rounding errors to avoid inaccuracies. It's often best to carry out calculations to several decimal places and round only at the final step.
Expanding on Percentage Concepts
Let's explore some related concepts that deepen your understanding of percentages:
Percentage Increase and Decrease
Calculating percentage increase or decrease involves finding the difference between two values and expressing that difference as a percentage of the original value. For instance, if a price increases from $50 to $60, the percentage increase is calculated as follows:
(60 - 50) / 50 x 100% = 20%
Similarly, a decrease from $60 to $50 represents a 16.67% decrease.
Percentage Points vs. Percentage Change
It's crucial to differentiate between percentage points and percentage change. A percentage point refers to an absolute difference between two percentages, while percentage change expresses the relative difference. For example, if interest rates increase from 5% to 10%, this is a 5 percentage point increase, but a 100% percentage change.
Finding the Original Value
Sometimes, you know the percentage and the final value and need to find the original value. For example, if an item is discounted by 44% and now costs $56, the original price can be found by using the following formula:
Original Price = Final Price / (1 - Discount Percentage) = $56 / (1 - 0.44) = $100
Advanced Percentage Calculations
As you progress, you might encounter more complex scenarios involving multiple percentages or compound interest. These often require a more in-depth understanding of mathematical concepts and might involve using formulas or spreadsheets.
Conclusion
Calculating "11 out of 25 as a percent" is a simple yet fundamental skill. Mastering this skill, along with a thorough understanding of the broader concepts of percentages, opens doors to numerous practical applications in various fields. By understanding the different methods—fraction method, proportion method, and using a calculator—and by avoiding common mistakes, you can confidently navigate the world of percentage calculations with ease. Remember that consistent practice is key to solidifying your understanding and building proficiency. The more you practice, the more comfortable and efficient you will become at handling percentage calculations.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 6 And 48
May 25, 2025
-
What Is The Percentage Of 70
May 25, 2025
-
What Is The Volume Of This Container
May 25, 2025
-
What Year Is A 22 Year Old Born
May 25, 2025
-
How Long Ago Was 2005 In Years
May 25, 2025
Related Post
Thank you for visiting our website which covers about 11 Out Of 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.