40 Of 35 Is What Number
listenit
May 24, 2025 · 4 min read
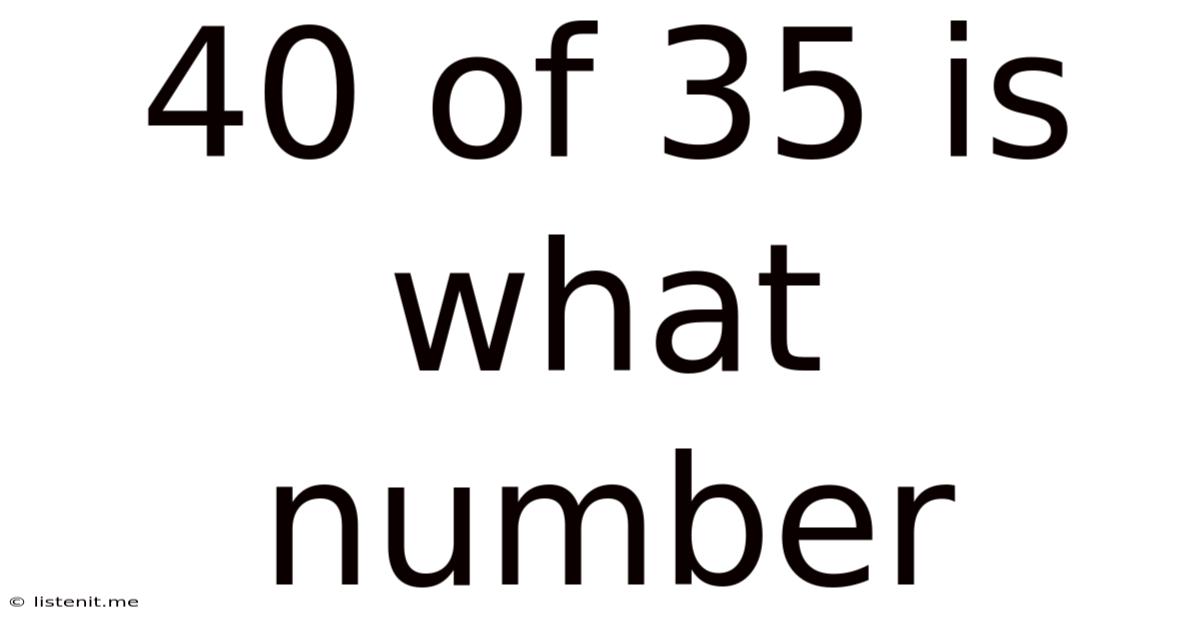
Table of Contents
Decoding Percentages: A Deep Dive into "40 of 35 is What Number?"
The question, "40 of 35 is what number?" might seem deceptively simple at first glance. It touches upon fundamental concepts of percentages, fractions, and ratios, all crucial elements in mathematics and everyday life. This article will not only answer the question directly but also explore the underlying mathematical principles, provide multiple methods for solving similar problems, and offer practical applications to solidify your understanding.
Understanding the Problem:
The phrase "40 of 35" implies a comparison or a ratio. We're looking for a quantity that represents 40 parts out of a total of 35 parts. This immediately suggests that we're dealing with a percentage greater than 100%, as we have more "parts" than the total. This scenario is common in various contexts, such as calculating growth rates, comparing quantities, and interpreting statistical data.
Method 1: Using Fractions
The most straightforward approach is to express the problem as a fraction:
- 40 out of 35 can be written as the fraction 40/35.
To simplify this fraction, we find the greatest common divisor (GCD) of 40 and 35, which is 5. Dividing both the numerator and the denominator by 5, we get:
- 40/35 = 8/7
This improper fraction (where the numerator is larger than the denominator) indicates a value greater than 1. To convert it to a mixed number (a whole number and a proper fraction), we perform the division:
- 8 ÷ 7 = 1 with a remainder of 1
Therefore, 8/7 can be expressed as 1 1/7. This means that 40 out of 35 is equal to 1 and 1/7.
Method 2: Using Percentages
While the fraction method provides a precise answer, understanding the percentage is equally important. To calculate the percentage, we follow these steps:
- Express the ratio as a fraction: 40/35
- Convert the fraction to a decimal: 40 ÷ 35 = 1.142857...
- Multiply the decimal by 100 to obtain the percentage: 1.142857... × 100 = 114.29% (approximately)
Therefore, 40 out of 35 represents approximately 114.29%. This confirms our understanding that the result is greater than 100%.
Method 3: Using Proportions
Another effective method involves setting up a proportion. We can represent the problem as:
- 40/35 = x/100
Where 'x' represents the percentage. To solve for x, we cross-multiply:
- 35x = 4000
- x = 4000/35
- x ≈ 114.29
This again shows that 40 out of 35 is approximately 114.29%.
Practical Applications:
Understanding this type of calculation has many practical applications across various fields:
- Business and Finance: Calculating growth rates (e.g., increase in sales, profits, or investments), understanding return on investment (ROI), and analyzing financial ratios.
- Science and Engineering: Determining experimental yields, expressing data as percentages, and comparing experimental results.
- Data Analysis: Calculating percentages in surveys, interpreting statistical data, and visualizing proportions.
- Everyday Life: Calculating tips, discounts, sales tax, and comparing prices.
Expanding the Concept: Handling Different Scenarios
The principles discussed above can be applied to similar problems with different numbers. Let's consider some variations:
-
Scenario 1: 25 of 50 is what number? This is a straightforward percentage problem, where 25/50 simplifies to 1/2 or 50%.
-
Scenario 2: 120 of 100 is what number? This problem results in a percentage greater than 100% (120%). The process remains the same: 120/100 = 1.2 = 120%.
-
Scenario 3: A store offers a 20% discount on a $100 item. What is the final price? This problem involves calculating a percentage decrease. A 20% discount means the final price will be 80% of the original price. Therefore, 0.80 x $100 = $80.
Advanced Concepts and Further Exploration
This seemingly basic mathematical operation opens the door to more complex concepts:
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. Understanding percentages is fundamental to mastering compound interest calculations.
- Statistical Analysis: Percentages are ubiquitous in statistical analysis. Understanding how to calculate and interpret them is crucial for drawing accurate conclusions from data.
- Financial Modeling: Financial models often rely heavily on percentage calculations for forecasting, risk assessment, and decision-making.
Conclusion:
The question "40 of 35 is what number?" isn't just a simple mathematical problem; it's a gateway to understanding fundamental concepts with far-reaching applications. By mastering the methods outlined in this article – using fractions, percentages, and proportions – you can confidently tackle similar problems and apply them to various real-world scenarios. Remember that understanding the underlying principles is as important as the numerical answer. The ability to work with percentages and ratios is a valuable skill applicable across numerous disciplines, making it a worthwhile investment of your time and effort. Continue practicing, and you'll find yourself easily navigating percentage-based calculations in any situation.
Latest Posts
Latest Posts
-
What Percentage Is 27 Out Of 35
May 24, 2025
-
What Is 72 In Fraction Form
May 24, 2025
-
Greatest Common Factor Of 12 And 45
May 24, 2025
-
What Is 30 Percent Of 30 Dollars
May 24, 2025
-
Calculate Dew Point From Wet And Dry Bulb
May 24, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 35 Is What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.