4 Out Of 18 As A Percentage
listenit
May 24, 2025 · 5 min read
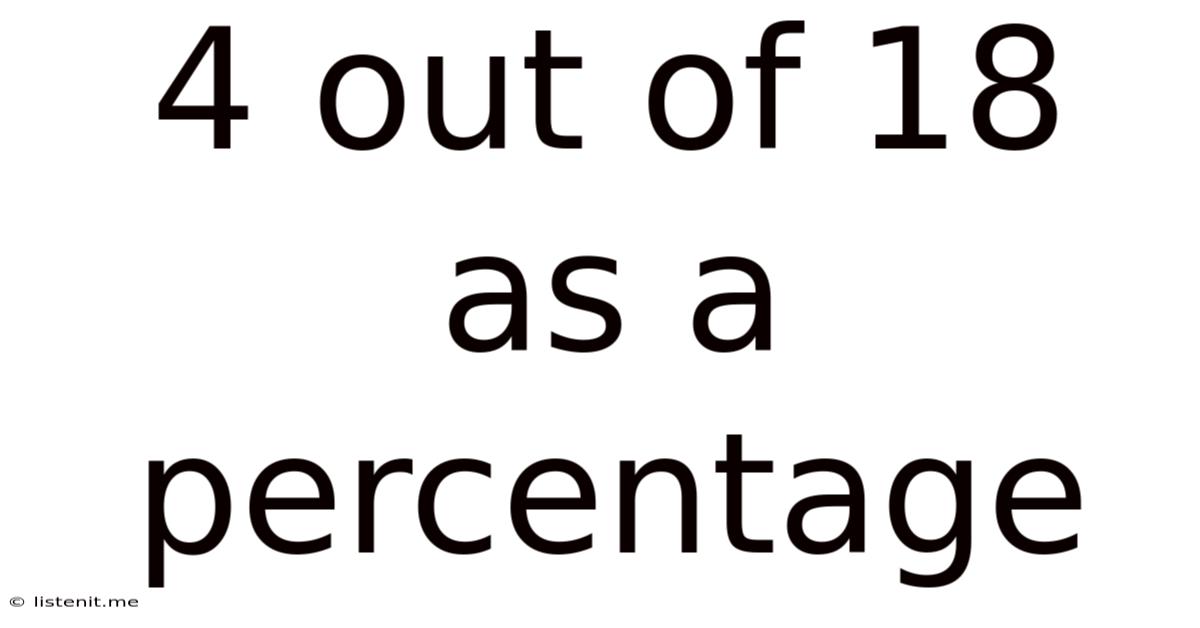
Table of Contents
4 out of 18 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in many aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide will delve deep into calculating the percentage that 4 out of 18 represents, explaining the process step-by-step and providing numerous examples and applications. We'll also explore various methods for solving this type of problem, equipping you with the knowledge to confidently tackle similar percentage calculations in the future.
Understanding the Fundamentals of Percentages
Before diving into the specific calculation of 4 out of 18 as a percentage, let's solidify our understanding of the core concepts. A percentage is simply a fraction expressed as a number out of 100. The word "percent" itself literally means "out of one hundred" (per centum in Latin). Therefore, any percentage can be represented as a fraction with a denominator of 100.
For example, 50% is equivalent to 50/100, which simplifies to 1/2 or 0.5. Understanding this fundamental relationship between percentages, fractions, and decimals is key to mastering percentage calculations.
Method 1: Using the Fraction Method
The most straightforward method to calculate 4 out of 18 as a percentage involves expressing the given numbers as a fraction and then converting that fraction to a percentage.
Step 1: Express as a Fraction:
The phrase "4 out of 18" directly translates to the fraction 4/18.
Step 2: Simplify the Fraction (Optional but Recommended):
Simplifying the fraction makes the subsequent calculations easier. We can simplify 4/18 by dividing both the numerator (4) and the denominator (18) by their greatest common divisor, which is 2. This gives us:
4/18 = 2/9
Step 3: Convert the Fraction to a Decimal:
To convert the simplified fraction 2/9 to a decimal, divide the numerator (2) by the denominator (9):
2 ÷ 9 ≈ 0.2222 (repeating decimal)
Step 4: Convert the Decimal to a Percentage:
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol:
0.2222 x 100 ≈ 22.22%
Therefore, 4 out of 18 is approximately 22.22%. The use of the approximately equal sign (≈) is because we're dealing with a repeating decimal. For most practical purposes, rounding to two decimal places is sufficient.
Method 2: Using Proportions
The proportion method offers an alternative approach to calculating percentages. This method is particularly useful when dealing with more complex percentage problems.
Step 1: Set up a Proportion:
We can set up a proportion to represent the problem:
4/18 = x/100
Here, 'x' represents the percentage we want to find.
Step 2: Cross-Multiply:
Cross-multiplying the proportion gives us:
18x = 400
Step 3: Solve for x:
To solve for 'x', divide both sides of the equation by 18:
x = 400/18 ≈ 22.22
Step 4: Express as a Percentage:
Therefore, x ≈ 22.22%, confirming the result obtained using the fraction method.
Method 3: Using a Calculator
Modern calculators are equipped with percentage functions, making percentage calculations incredibly quick and easy. Simply enter 4 ÷ 18 and then multiply the result by 100 to obtain the percentage. Most calculators will display the result directly as a percentage.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in a multitude of real-world scenarios. Here are a few examples:
-
Academic Performance: Imagine a student scoring 4 out of 18 on a quiz. Calculating the percentage (22.22%) provides a clear understanding of their performance relative to the total possible marks.
-
Sales and Discounts: Retailers frequently offer discounts expressed as percentages. Understanding percentages allows consumers to calculate the actual discount amount and the final price.
-
Financial Analysis: In finance, percentages are used extensively to analyze investment returns, interest rates, and other financial metrics.
-
Statistical Analysis: Percentages are crucial in expressing proportions and probabilities in various statistical analyses, including surveys, polls, and research studies.
-
Data Interpretation: In many fields, data is often presented in the form of percentages to facilitate easy interpretation and comparison.
Beyond the Basics: Dealing with More Complex Scenarios
While this article focuses primarily on calculating 4 out of 18 as a percentage, the underlying principles and methods can be applied to a wider range of percentage problems. For example, you might encounter situations where:
-
The numbers are larger or involve decimals: The same methods apply; just be mindful of using your calculator carefully.
-
You need to calculate a percentage increase or decrease: These problems involve finding the difference between two values and expressing that difference as a percentage of the original value.
-
You need to work backward from a percentage to find the original value: This requires understanding the inverse relationship between percentages and their corresponding fractions or decimals.
Mastering Percentage Calculations: Tips and Practice
Mastering percentage calculations takes practice. Here are a few tips to improve your skills:
-
Practice regularly: Work through various percentage problems of increasing complexity.
-
Understand the different methods: Familiarize yourself with the fraction, proportion, and calculator methods to choose the approach that suits you best.
-
Pay attention to detail: Ensure you're correctly entering numbers and performing calculations.
-
Check your answers: Verify your calculations to ensure accuracy.
Conclusion
Calculating 4 out of 18 as a percentage, which is approximately 22.22%, is a straightforward process once you understand the fundamental principles of percentages. This guide has explored three different methods for achieving this calculation, highlighting their practical applications and emphasizing the importance of percentage calculations in various aspects of life. By mastering these techniques, you'll be well-equipped to tackle a wide range of percentage problems with confidence and accuracy, ultimately improving your analytical and problem-solving skills. Remember to practice regularly to solidify your understanding and build fluency in this essential mathematical skill.
Latest Posts
Latest Posts
-
What Is 2 7 In A Fraction
May 24, 2025
-
88 As A Product Of Prime Factors
May 24, 2025
-
How To Calculate 9 Hole Handicap
May 24, 2025
-
What Is 15 Percent Of 16
May 24, 2025
-
412 Out Of 500 In Percentage
May 24, 2025
Related Post
Thank you for visiting our website which covers about 4 Out Of 18 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.