4 Copies Of 1 5 Is
listenit
May 25, 2025 · 5 min read
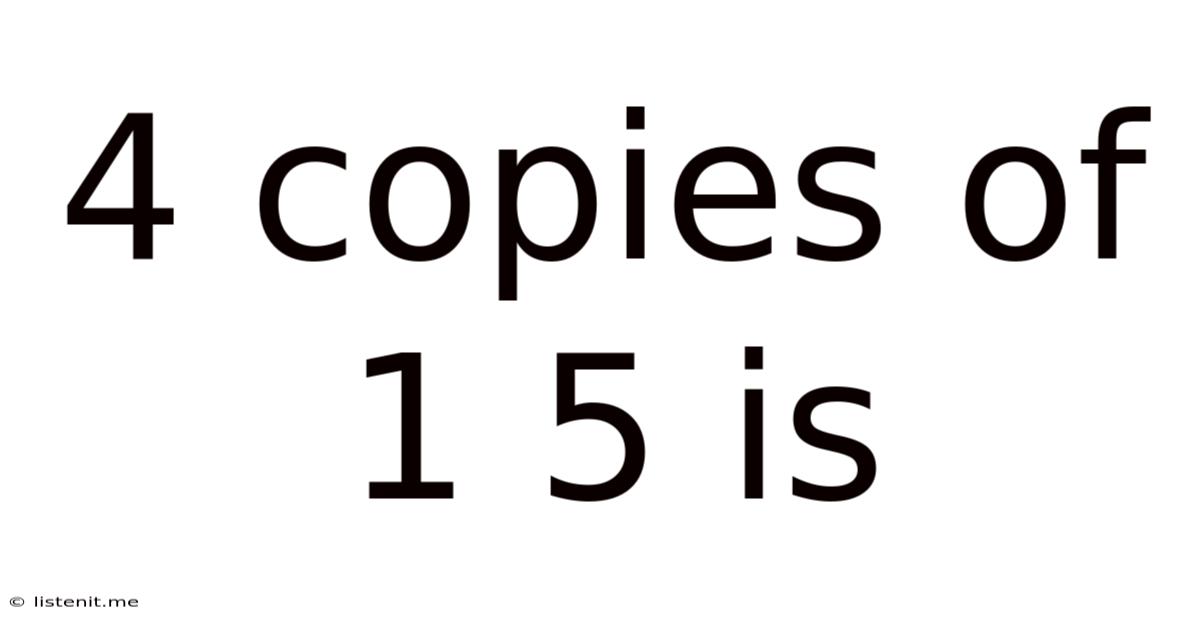
Table of Contents
4 Copies of 1/5 Is: Exploring Fractions, Decimals, and Percentages
The seemingly simple question, "4 copies of 1/5 is...?" opens a door to a rich exploration of fundamental mathematical concepts. While the immediate answer might seem obvious, delving deeper reveals interconnectedness between fractions, decimals, and percentages, crucial building blocks for more advanced mathematical understanding. This article will unpack this seemingly simple problem, demonstrating its multifaceted nature and highlighting its significance in everyday life and various academic disciplines.
Understanding Fractions: The Building Blocks
Before tackling the core question, it's crucial to grasp the concept of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates the number of parts being considered. In our case, 1/5 signifies one part out of a total of five equal parts.
Visualizing 1/5
Imagine a pizza cut into five equal slices. 1/5 represents one of those slices. To understand "4 copies of 1/5," visualize taking four of these slices. This visual representation helps solidify the concept and makes it more intuitive, particularly for beginners.
Calculating 4 Copies of 1/5
The question "4 copies of 1/5 is...?" is essentially asking us to add 1/5 to itself four times: 1/5 + 1/5 + 1/5 + 1/5. Since the denominators are the same, we can simply add the numerators: (1 + 1 + 1 + 1)/5 = 4/5.
Therefore, 4 copies of 1/5 is 4/5.
Alternative Approach: Multiplication
Instead of repeated addition, we can use multiplication. "4 copies of 1/5" is mathematically equivalent to 4 x (1/5). When multiplying a whole number by a fraction, we multiply the whole number by the numerator and keep the denominator the same: 4 x 1/5 = (4 x 1)/5 = 4/5. This approach is more efficient, particularly when dealing with larger numbers of copies.
Converting Fractions to Decimals: Expanding the Understanding
Fractions and decimals are two different ways of representing the same value. To convert a fraction to a decimal, we divide the numerator by the denominator. In our case, converting 4/5 to a decimal involves dividing 4 by 5: 4 ÷ 5 = 0.8.
Therefore, 4 copies of 1/5 is also equal to 0.8.
Converting Fractions to Percentages: A Practical Application
Percentages are another way of expressing fractions and decimals, representing parts per hundred. To convert a fraction or decimal to a percentage, we multiply by 100 and add the percent symbol (%).
Converting 4/5 to a percentage: (4/5) x 100% = 0.8 x 100% = 80%.
Alternatively, starting from the decimal 0.8: 0.8 x 100% = 80%.
Therefore, 4 copies of 1/5 is also equal to 80%.
Real-World Applications: Connecting Math to Everyday Life
Understanding fractions, decimals, and percentages is not just an academic exercise; it's essential for navigating everyday situations. Here are some examples:
-
Shopping: Calculating discounts, sales tax, and unit prices often involve working with fractions, decimals, and percentages. For example, if an item is 20% off, understanding this means a 1/5 reduction in price.
-
Cooking: Recipes frequently use fractions (e.g., 1/2 cup of flour, 1/4 teaspoon of salt). Scaling recipes up or down requires understanding how to multiply and divide fractions.
-
Finance: Understanding interest rates, loan payments, and investment returns relies heavily on percentages and decimal calculations.
-
Measurement: Many measurements involve fractions (e.g., 1/8 inch, 3/4 mile). Converting these fractions to decimals or percentages can be necessary depending on the context.
-
Data Analysis: Representing data visually and interpreting statistical information often requires working with fractions, decimals, and percentages.
Beyond the Basics: Exploring More Complex Scenarios
While the initial problem seems simple, it lays the groundwork for tackling more complex fractional calculations. Consider the following extensions:
-
Multiplying fractions: What if we wanted to find "3/4 copies of 1/5"? This would involve multiplying fractions: (3/4) x (1/5) = 3/20.
-
Mixed numbers: What if the "copies" were represented as a mixed number, like 2 1/2 copies of 1/5? This involves converting the mixed number to an improper fraction and then multiplying.
-
Dividing fractions: What if we had 4/5 and wanted to find out how many 1/5s it contains? This involves dividing fractions: (4/5) ÷ (1/5) = 4.
The Importance of Mastering Fractions, Decimals, and Percentages
The ability to seamlessly convert between fractions, decimals, and percentages is crucial for success in mathematics and its application to real-world problems. This proficiency is not only valuable for everyday tasks but also serves as a fundamental building block for more advanced mathematical concepts, including algebra, calculus, and statistics. A solid understanding of these foundational concepts builds a strong base for future learning.
Conclusion: A Simple Problem with Profound Implications
The seemingly trivial question, "4 copies of 1/5 is...?" reveals the interconnectedness of fundamental mathematical concepts and their practical applications in our daily lives. By exploring this seemingly simple problem, we have touched upon fractions, decimals, percentages, and various methods of calculation. This understanding forms a solid foundation for navigating more complex mathematical challenges and effectively applying mathematical reasoning to real-world scenarios. Mastering these skills empowers individuals to confidently approach quantitative challenges, leading to greater success in various academic and professional endeavors. From calculating discounts to understanding financial reports, the ability to work with fractions, decimals, and percentages is an invaluable asset in today's world.
Latest Posts
Latest Posts
-
What Number Multiplied By 3 5 Has A Product Of 1
May 25, 2025
-
30 Days From July 27 2024
May 25, 2025
-
1 Out Of 17 As A Percentage
May 25, 2025
-
How Old Am I Born In 1985
May 25, 2025
-
5 Out Of 24 As A Percentage
May 25, 2025
Related Post
Thank you for visiting our website which covers about 4 Copies Of 1 5 Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.