What Number Multiplied By 3/5 Has A Product Of 1
listenit
May 25, 2025 · 4 min read
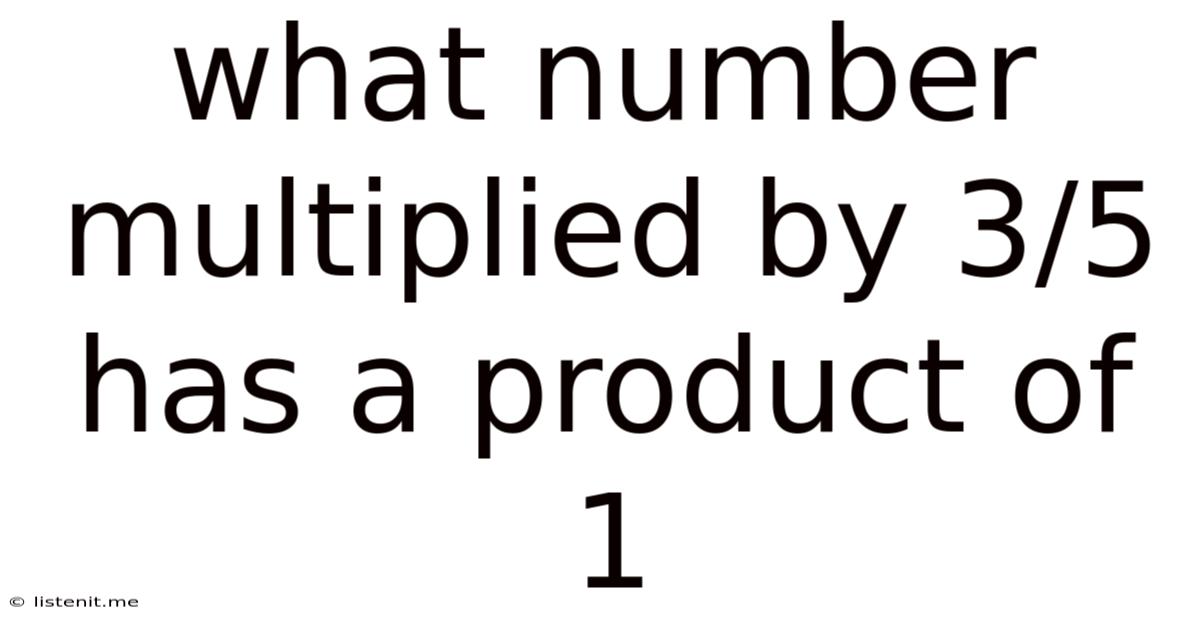
Table of Contents
What Number Multiplied by 3/5 Has a Product of 1? Unlocking the Secrets of Reciprocals
Finding the number that, when multiplied by 3/5, results in a product of 1 might seem like a simple arithmetic problem. However, this seemingly straightforward question opens a door to a deeper understanding of fundamental mathematical concepts, including reciprocals, multiplicative inverses, and the identity property of multiplication. This article will delve into this problem, exploring different solution methods and highlighting the broader mathematical principles involved. We'll also look at how to solve similar problems and apply these concepts in more complex scenarios.
Understanding the Problem: Finding the Multiplicative Inverse
The core of the problem lies in finding the multiplicative inverse, also known as the reciprocal, of 3/5. The multiplicative inverse of a number is the number that, when multiplied by the original number, yields 1 (the multiplicative identity). In simpler terms, we're looking for a number that "undoes" the multiplication by 3/5.
Method 1: Using the Definition of Reciprocals
The most straightforward approach is to directly apply the definition of a reciprocal. If we let 'x' represent the unknown number, we can express the problem as an equation:
(3/5) * x = 1
To solve for 'x', we need to isolate it. We can do this by dividing both sides of the equation by 3/5:
x = 1 / (3/5)
Remember that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of 3/5 is 5/3. Therefore:
x = 1 * (5/3) = 5/3
Therefore, the number that, when multiplied by 3/5, gives a product of 1 is 5/3.
Method 2: Cross-Multiplication
Another way to solve this is through cross-multiplication. We can rewrite the equation (3/5) * x = 1 as a proportion:
3/5 = 1/x
Now, cross-multiply:
3 * x = 5 * 1
3x = 5
Divide both sides by 3:
x = 5/3
Again, we arrive at the solution: x = 5/3. This method provides an alternative approach to solving similar problems, especially those involving proportions.
Method 3: Intuitive Understanding
Let's approach this from a more intuitive perspective. We know that multiplying a fraction by its reciprocal always results in 1. This is a direct consequence of the definition of reciprocals and the commutative property of multiplication.
Consider the fraction 3/5. Its reciprocal is obtained by swapping the numerator and the denominator: 5/3. If we multiply these two fractions:
(3/5) * (5/3) = (3 * 5) / (5 * 3) = 15/15 = 1
This reinforces the fact that 5/3 is the multiplicative inverse of 3/5.
The Identity Property of Multiplication
The number 1 plays a crucial role in this problem. It's the multiplicative identity, meaning that any number multiplied by 1 remains unchanged. The entire process of finding the reciprocal is essentially about finding a number that, when multiplied by the original number, results in this multiplicative identity.
Extending the Concept: Finding Reciprocals of Other Numbers
The methods outlined above can be applied to find the reciprocals of other numbers, both fractions and integers.
Example 1: Finding the reciprocal of 2/7
The reciprocal of 2/7 is 7/2. (2/7) * (7/2) = 1
Example 2: Finding the reciprocal of 5
The integer 5 can be written as the fraction 5/1. Its reciprocal is therefore 1/5. (5/1) * (1/5) = 1
Example 3: Finding the reciprocal of a decimal:
Let's find the reciprocal of 0.25. First convert the decimal into a fraction: 0.25 = 1/4. The reciprocal of 1/4 is 4/1 or simply 4. (1/4) * 4 = 1
Applications in Real-World Problems
The concept of reciprocals and multiplicative inverses finds applications in various fields, including:
-
Physics: Calculating inverse relationships, like the relationship between speed and time (speed = distance/time, therefore time = distance/speed).
-
Engineering: Solving problems involving ratios and proportions in design and construction.
-
Finance: Calculating interest rates and loan payments.
-
Computer Science: Working with inverse matrices in computer graphics and other applications.
Solving More Complex Problems
The principles discussed here can be extended to solve more complex equations involving fractions and reciprocals. For example:
(2/3)x + (1/2) = 5/6
First, subtract 1/2 from both sides:
(2/3)x = 5/6 - 1/2
Find a common denominator (6):
(2/3)x = 5/6 - 3/6 = 2/6 = 1/3
Now, multiply both sides by the reciprocal of 2/3, which is 3/2:
x = (1/3) * (3/2) = 1/2
Therefore, the solution is x = 1/2. This shows how the understanding of reciprocals is crucial in solving more complex algebraic equations.
Conclusion: Mastering Reciprocals for Mathematical Proficiency
Understanding the concept of reciprocals and how to find them is a fundamental skill in mathematics. This article has explored multiple approaches to solving the problem of finding the number that, when multiplied by 3/5, equals 1, highlighting the importance of reciprocals in various mathematical contexts and their applications in real-world scenarios. By mastering these concepts, you'll not only be able to solve similar problems with ease but also enhance your overall mathematical proficiency, laying a solid foundation for tackling more advanced mathematical challenges. Remember the power of reciprocals – they are the keys to unlocking many mathematical doors!
Latest Posts
Latest Posts
-
2 Hour 22 Minute Marathon Pace
May 25, 2025
-
14 Divided By 6 As A Fraction
May 25, 2025
-
1 Day 6 Hours From Now
May 25, 2025
-
3 2 4 As An Improper Fraction
May 25, 2025
-
Greatest Common Factor Of 63 And 49
May 25, 2025
Related Post
Thank you for visiting our website which covers about What Number Multiplied By 3/5 Has A Product Of 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.