3x 4y 12 Slope Intercept Form
listenit
May 12, 2025 · 6 min read
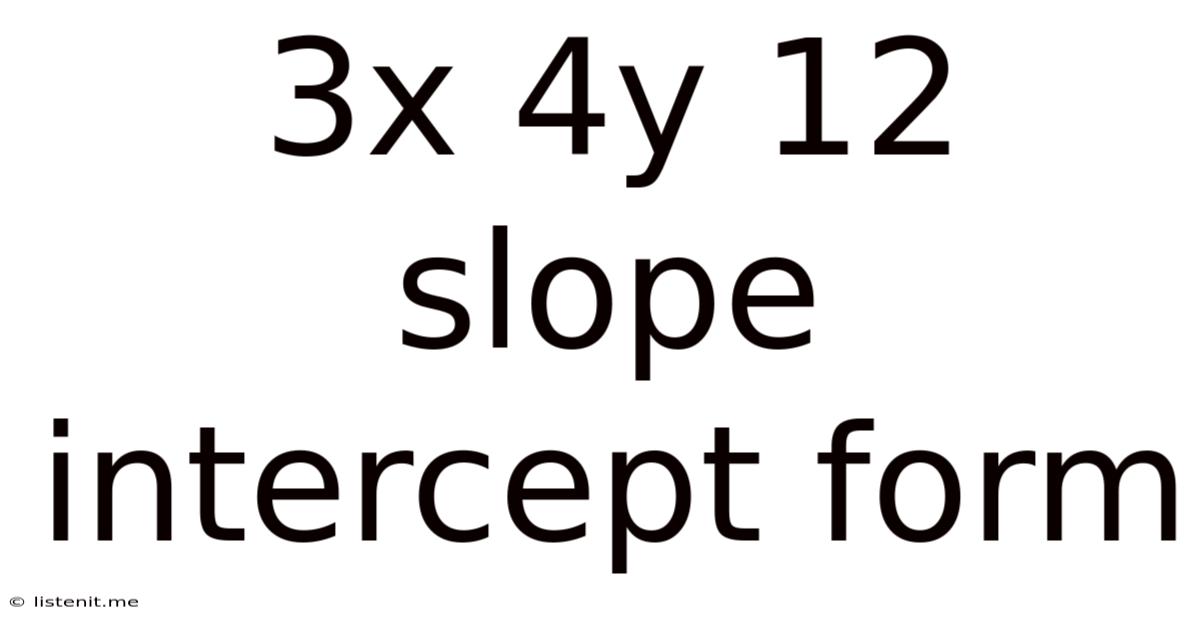
Table of Contents
Unveiling the Secrets of the 3x + 4y = 12 Equation: A Deep Dive into Slope-Intercept Form
The equation 3x + 4y = 12 might seem simple at first glance, but it holds a wealth of information about a straight line. Understanding how to transform this equation into slope-intercept form (y = mx + b) unlocks its secrets, revealing its slope, y-intercept, and ultimately, its graphical representation. This comprehensive guide will explore this transformation, delve into the significance of the slope and y-intercept, and show you how to apply this knowledge to various mathematical problems.
From Standard Form to Slope-Intercept Form: The Transformation
The equation 3x + 4y = 12 is in standard form (Ax + By = C), where A, B, and C are constants. While useful in certain contexts, the standard form doesn't immediately reveal the line's slope and y-intercept. To uncover these crucial pieces of information, we need to convert it to slope-intercept form (y = mx + b), where 'm' represents the slope and 'b' represents the y-intercept.
The transformation is straightforward: we simply solve for 'y'. Let's break down the steps:
-
Isolate the 'y' term: Subtract 3x from both sides of the equation: 4y = -3x + 12
-
Solve for 'y': Divide both sides of the equation by 4: y = (-3/4)x + 3
Now, we have our equation in slope-intercept form: y = (-3/4)x + 3.
Deciphering the Slope and Y-Intercept
With the equation in slope-intercept form, we can readily identify the slope and y-intercept:
-
Slope (m): The slope, -3/4, indicates the steepness and direction of the line. A negative slope means the line is decreasing (sloping downwards) as we move from left to right. The numerical value, 3/4, signifies that for every 4 units of horizontal movement to the right, the line drops 3 units vertically.
-
Y-intercept (b): The y-intercept, 3, represents the point where the line intersects the y-axis. This means the line passes through the point (0, 3).
Graphical Representation: Bringing the Line to Life
Now that we've determined the slope and y-intercept, we can easily graph the line. We start by plotting the y-intercept (0, 3) on the Cartesian plane. Then, using the slope (-3/4), we can find another point on the line. Remember, the slope is the ratio of the vertical change (rise) to the horizontal change (run).
From the y-intercept (0, 3), we can move 4 units to the right (run) and 3 units down (rise, since the slope is negative) to find another point on the line: (4, 0). Connecting these two points gives us the graph of the line represented by the equation 3x + 4y = 12.
Visualizing the Slope and Intercept: A Deeper Understanding
The graphical representation allows for a more intuitive understanding of the slope and y-intercept. The y-intercept is visually apparent as the point where the line crosses the y-axis. The slope is reflected in the angle of the line; a steeper line indicates a larger (positive or negative) slope, while a flatter line indicates a smaller slope.
Applications and Extensions: Beyond the Basics
The knowledge gained from transforming the equation 3x + 4y = 12 into slope-intercept form has numerous applications in various mathematical and real-world scenarios.
1. Finding Intercepts: Where the Line Meets the Axes
We've already found the y-intercept. To find the x-intercept (where the line crosses the x-axis), we simply set y = 0 in the original equation:
3x + 4(0) = 12 3x = 12 x = 4
Therefore, the x-intercept is (4, 0). This confirms the point we found using the slope earlier.
2. Determining Parallel and Perpendicular Lines
The slope plays a crucial role in determining the relationship between lines.
-
Parallel Lines: Parallel lines have the same slope. Any line parallel to the line represented by 3x + 4y = 12 will also have a slope of -3/4.
-
Perpendicular Lines: Perpendicular lines have slopes that are negative reciprocals of each other. The negative reciprocal of -3/4 is 4/3. Any line perpendicular to the line represented by 3x + 4y = 12 will have a slope of 4/3.
3. Solving Systems of Equations: Finding Points of Intersection
The slope-intercept form is invaluable when solving systems of linear equations. By graphing both lines, the point of intersection represents the solution to the system. Alternatively, we can solve the system algebraically using substitution or elimination methods.
4. Real-World Applications: Modeling Linear Relationships
Linear equations, like 3x + 4y = 12, are used extensively to model linear relationships in various real-world scenarios. For example:
-
Cost analysis: The equation could represent the total cost (y) of producing x units of a product, where 3x represents variable costs and 4y represents fixed costs.
-
Resource allocation: The equation might model the allocation of resources (x and y) subject to a constraint (the total resources available represented by 12).
-
Distance-time relationships: In a simplified scenario, the equation could represent a relationship between distance (x) and time (y) for a moving object with certain constraints.
Advanced Concepts and Further Exploration
While the transformation to slope-intercept form provides a clear understanding of the line, further explorations can enhance our mathematical proficiency.
1. Different Forms of Linear Equations: Expanding Our Toolkit
Understanding other forms of linear equations, such as point-slope form and two-point form, expands our ability to represent lines effectively depending on the information available.
2. Working with Inequalities: Shading Regions on the Plane
Instead of an equation, we might encounter inequalities like 3x + 4y ≤ 12. This represents a region on the Cartesian plane rather than a single line. Graphing the line 3x + 4y = 12 and then shading the appropriate region based on the inequality symbol is crucial for solving inequality problems.
3. Linear Programming: Optimization using Linear Constraints
Linear programming involves optimizing an objective function subject to linear constraints. Understanding the graphical representation of linear equations is vital for visualizing the feasible region and finding optimal solutions.
4. Multivariable Linear Equations: Stepping into Higher Dimensions
While this article focuses on two variables, linear equations can extend to higher dimensions. Similar principles apply in these cases, but the graphical representation becomes more complex, often requiring three-dimensional visualization or other techniques.
Conclusion: Mastering the Fundamentals and Beyond
The seemingly straightforward equation 3x + 4y = 12 serves as a springboard to a deeper understanding of linear equations. By mastering the conversion to slope-intercept form, identifying the slope and y-intercept, and visualizing the graphical representation, we unlock the power of this fundamental concept in mathematics and its applications across various fields. The journey from a simple equation to a comprehensive understanding of its implications highlights the beauty and utility of linear algebra. Continue exploring these concepts, and you'll find yourself equipped to tackle increasingly complex mathematical problems with confidence and finesse. This fundamental knowledge forms the bedrock for more advanced mathematical studies. Remember to practice consistently to reinforce your learning and unlock the full potential of your mathematical abilities.
Latest Posts
Latest Posts
-
Bosss Or Boss Which Is Correct
May 12, 2025
-
X 2 Xy Y 2 Factor
May 12, 2025
-
Reaction Of Hydrogen And Nitrogen To Form Ammonia
May 12, 2025
-
How To Determine Horizontal And Vertical Asymptotes
May 12, 2025
-
Plants Make Their Own Food Therefore They Are Classified As
May 12, 2025
Related Post
Thank you for visiting our website which covers about 3x 4y 12 Slope Intercept Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.