X 2 Xy Y 2 Factor
listenit
May 12, 2025 · 5 min read
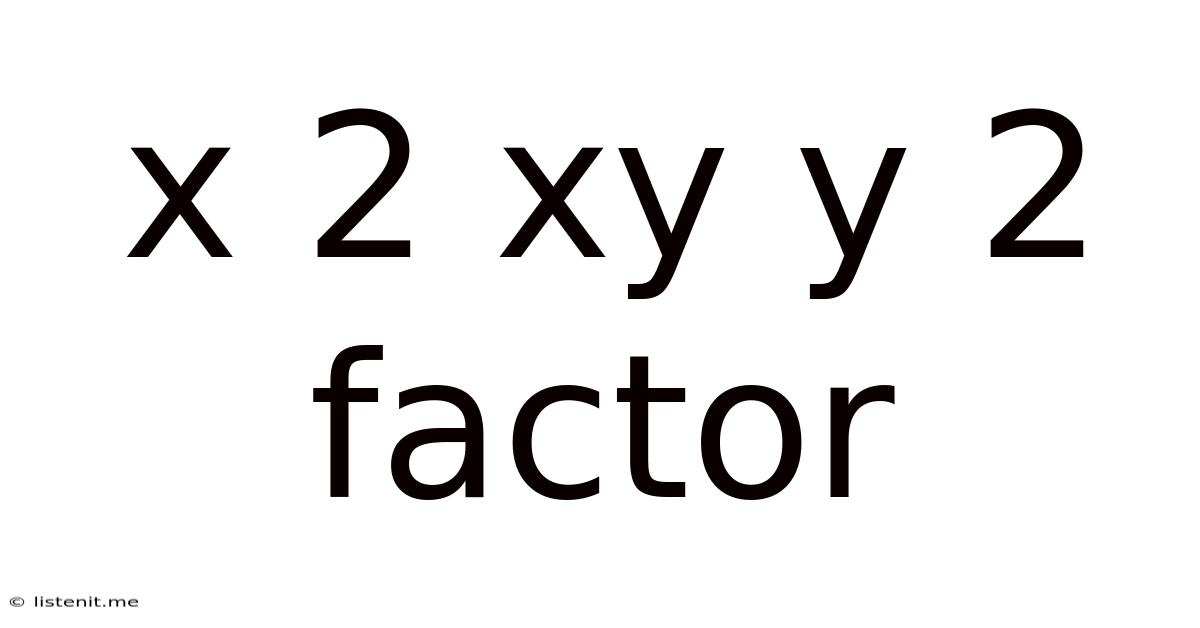
Table of Contents
Factoring x² + 2xy + y²: A Comprehensive Guide
The expression x² + 2xy + y² is a classic example of a perfect square trinomial. Understanding how to factor this expression is fundamental to success in algebra and beyond. This comprehensive guide will explore various methods for factoring x² + 2xy + y², explain the underlying principles, and delve into related concepts to solidify your understanding.
Understanding Perfect Square Trinomials
Before diving into the factoring process, let's define what a perfect square trinomial is. A perfect square trinomial is a trinomial (a three-term polynomial) that can be factored into the square of a binomial. The general form is:
a² + 2ab + b² = (a + b)²
or
a² - 2ab + b² = (a - b)²
In our case, x² + 2xy + y², we can see that:
- a = x
- b = y
- 2ab = 2xy
This clearly fits the pattern of a perfect square trinomial, making it easily factorable.
Method 1: Recognizing the Pattern
The most straightforward method is to recognize the perfect square trinomial pattern directly. Once you identify 'a' and 'b', you can immediately write the factored form:
(x + y)²
This method is quick and efficient once you become familiar with recognizing the pattern. However, it's crucial to understand why this works, which we'll delve into further.
Method 2: FOIL Method in Reverse
The FOIL method (First, Outer, Inner, Last) is typically used for multiplying binomials. We can reverse this process to factor the trinomial. Let's consider two binomials: (x + a)(x + b). Expanding this using FOIL gives:
x² + ax + bx + ab = x² + (a + b)x + ab
Comparing this to our expression x² + 2xy + y², we can see:
- The coefficient of x² is 1.
- The coefficient of x is 2y.
- The constant term is y².
We need to find two numbers ('a' and 'b') that add up to 2y and multiply to y². Clearly, a = y and b = y satisfy these conditions. Therefore, the factored form is:
(x + y)(x + y) = (x + y)²
This method reinforces the understanding of the underlying relationships between the coefficients of the trinomial and the terms in its binomial factors.
Method 3: Completing the Square
Completing the square is a more general technique used for factoring quadratic expressions, even those that aren't perfect square trinomials. However, it's particularly straightforward for this case.
-
Group the x terms: We start with x² + 2xy + y². Notice that y² is a constant.
-
Focus on the x terms: Consider x² + 2xy. To complete the square, we need to add and subtract a term that makes this expression a perfect square. Half of the coefficient of the x term (2y) is y, and squaring it gives y². So we add and subtract y²:
x² + 2xy + y² - y² + y²
-
Factor the perfect square: The first three terms form a perfect square trinomial:
(x + y)² - y² + y²
-
Simplify: The -y² and +y² cancel out, leaving:
(x + y)²
This method provides a more systematic approach to factoring, which is helpful when dealing with more complex quadratic expressions.
Why is (x + y)² equal to x² + 2xy + y²?
Let's explicitly demonstrate why the binomial expansion of (x + y)² results in x² + 2xy + y². This is achieved using the distributive property (often called FOIL):
(x + y)² = (x + y)(x + y)
Applying the distributive property:
= x(x + y) + y(x + y)
= x² + xy + yx + y²
= x² + 2xy + y²
This demonstrates the equivalence conclusively.
Applications of Factoring x² + 2xy + y²
The ability to factor x² + 2xy + y² has numerous applications in various areas of mathematics and beyond:
-
Simplifying algebraic expressions: Factoring can simplify complex expressions, making them easier to manipulate and solve.
-
Solving quadratic equations: Factoring is a fundamental technique for solving quadratic equations. If you encounter a quadratic equation that can be expressed in the form x² + 2xy + y² = 0, factoring allows you to easily find solutions.
-
Calculus: In calculus, factoring is essential for simplifying expressions, finding derivatives, and evaluating integrals. Many calculus problems involve expressions similar to x² + 2xy + y², and the ability to factor them efficiently is crucial.
-
Geometry and Physics: In geometry and physics, quadratic equations often arise when dealing with problems involving areas, distances, and trajectories. Factoring plays a critical role in solving these equations.
-
Computer Science: In computer science, factoring is used in algorithm design and optimization. Efficient factoring algorithms are crucial for cryptographic applications and data analysis.
Extending the Concept: Variations and Related Problems
While we've focused on x² + 2xy + y², the underlying principles extend to other similar expressions. Consider these variations:
-
(x - y)² = x² - 2xy + y²: This is the other common perfect square trinomial. The only difference is the negative sign in the middle term, resulting in a subtraction within the binomial.
-
(ax + by)² = a²x² + 2abxy + b²y²: This demonstrates how the concept applies with coefficients. Recognizing the pattern of a perfect square trinomial remains key.
-
Factoring expressions with a common factor: Sometimes, an expression might contain a common factor that can be factored out before applying the perfect square trinomial method. For example, 2x² + 4xy + 2y² can be factored as 2(x² + 2xy + y²) = 2(x + y)².
Conclusion
Factoring x² + 2xy + y² is a fundamental skill in algebra. Understanding the concept of perfect square trinomials, employing different factoring methods, and grasping their practical applications across diverse fields are essential for building a strong mathematical foundation. By mastering this concept, you'll be well-prepared to tackle more complex algebraic problems and broaden your understanding of mathematical principles. Remember to practice regularly to enhance your speed and accuracy in recognizing and factoring perfect square trinomials. The more you practice, the more intuitive this process will become.
Latest Posts
Latest Posts
-
How Do You Calculate The Mass Of A Liquid
May 13, 2025
-
How To Find Value Of X When Y Is Given
May 13, 2025
-
Is Algae A Producer Consumer Or Decomposer
May 13, 2025
-
What Is The Si Unit Of Kinetic Energy
May 13, 2025
-
Melting Point Of Gold In Celsius
May 13, 2025
Related Post
Thank you for visiting our website which covers about X 2 Xy Y 2 Factor . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.