3x 2y 16 In Slope Intercept Form
listenit
Apr 04, 2025 · 5 min read
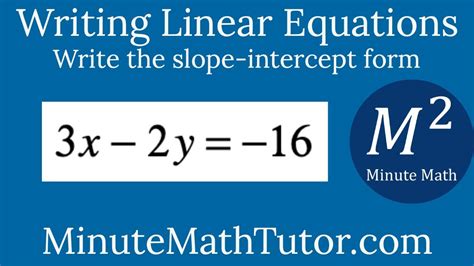
Table of Contents
Converting 3x + 2y = 16 to Slope-Intercept Form: A Comprehensive Guide
The equation 3x + 2y = 16 represents a straight line. While useful in its current form, converting it to slope-intercept form (y = mx + b) offers significant advantages in understanding and visualizing the line's characteristics. This form reveals the slope (m) and the y-intercept (b) immediately, making it easier to graph and analyze. This comprehensive guide will walk you through the process, explaining each step and providing additional context for a thorough understanding.
Understanding Slope-Intercept Form (y = mx + b)
Before diving into the conversion, let's solidify our understanding of the slope-intercept form, y = mx + b.
- y: Represents the y-coordinate of any point on the line.
- x: Represents the x-coordinate of any point on the line.
- m: Represents the slope of the line. The slope describes the steepness and direction of the line. A positive slope indicates an upward trend from left to right, while a negative slope indicates a downward trend. A slope of zero represents a horizontal line, and an undefined slope represents a vertical line.
- b: Represents the y-intercept. This is the point where the line crosses the y-axis (where x = 0).
Converting 3x + 2y = 16 to Slope-Intercept Form
The goal is to isolate 'y' on one side of the equation. Here's a step-by-step breakdown:
Step 1: Subtract 3x from both sides:
Our starting equation is: 3x + 2y = 16
Subtracting 3x from both sides gives us:
2y = -3x + 16
Step 2: Divide both sides by 2:
To isolate 'y', we divide both sides of the equation by 2:
y = (-3/2)x + 16/2
Step 3: Simplify:
Simplifying the fractions, we arrive at the slope-intercept form:
y = (-3/2)x + 8
This is the final equation in slope-intercept form.
Interpreting the Results: Slope and y-intercept
Now that we have the equation in slope-intercept form, we can easily identify the slope and y-intercept:
-
Slope (m) = -3/2: This indicates a negative slope, meaning the line slopes downwards from left to right. The magnitude of the slope (3/2) represents the steepness of the line – for every 2 units of horizontal movement, the line moves 3 units downwards.
-
y-intercept (b) = 8: This means the line intersects the y-axis at the point (0, 8).
Graphing the Line
With the slope and y-intercept, graphing the line becomes straightforward:
-
Plot the y-intercept: Start by plotting the point (0, 8) on the y-axis.
-
Use the slope to find another point: The slope is -3/2. This can be interpreted as a rise of -3 (down 3 units) and a run of 2 (right 2 units). Starting from the y-intercept (0, 8), move down 3 units and right 2 units. This gives you another point on the line, (2, 5).
-
Draw the line: Draw a straight line passing through the two points (0, 8) and (2, 5). This line represents the equation 3x + 2y = 16.
Applications and Further Exploration
Understanding the slope-intercept form is crucial in various applications:
-
Linear Regression: In statistics, linear regression aims to find the best-fitting line through a set of data points. The resulting equation is often expressed in slope-intercept form to understand the relationship between variables.
-
Physics and Engineering: Many physical phenomena are modeled using linear equations, such as the relationship between distance and time in constant velocity motion. The slope represents velocity, and the y-intercept represents the initial position.
-
Economics: Supply and demand curves in economics are often represented using linear equations. The slope indicates the sensitivity of supply or demand to changes in price.
-
Computer Graphics: Lines are fundamental elements in computer graphics. The slope-intercept form is used extensively to draw and manipulate lines efficiently.
Alternative Methods for Finding the Slope and Intercept
While converting to slope-intercept form is the most direct method, there are alternative approaches to determine the slope and y-intercept:
1. Using Two Points:
If you have two points that lie on the line, you can calculate the slope using the formula:
m = (y₂ - y₁) / (x₂ - x₁)
where (x₁, y₁) and (x₂, y₂) are the coordinates of the two points. Once you have the slope, you can use the point-slope form of the equation (y - y₁ = m(x - x₁)) to find the equation of the line and then convert it to slope-intercept form.
2. Using the x-intercept:
The x-intercept is the point where the line crosses the x-axis (where y = 0). To find the x-intercept, substitute y = 0 into the original equation and solve for x. This gives you one point on the line. You can then use this point and the y-intercept to calculate the slope, as described above.
Advanced Considerations: Parallel and Perpendicular Lines
Understanding the slope-intercept form also aids in determining relationships between lines:
-
Parallel Lines: Parallel lines have the same slope (m) but different y-intercepts (b). If you have a line in slope-intercept form and need to find the equation of a parallel line passing through a given point, simply use the same slope and substitute the coordinates of the given point into the point-slope form to find the equation of the parallel line.
-
Perpendicular Lines: Perpendicular lines have slopes that are negative reciprocals of each other. If the slope of one line is m, the slope of a perpendicular line is -1/m. Again, the point-slope form is useful for finding the equation of a perpendicular line passing through a given point.
Conclusion: Mastering Slope-Intercept Form
Converting the equation 3x + 2y = 16 to slope-intercept form (y = (-3/2)x + 8) allows for a much clearer understanding of the line's characteristics. The slope and y-intercept provide valuable information for graphing, analysis, and applications in various fields. Mastering this conversion and understanding its implications is a fundamental skill in algebra and beyond. Remember to practice these steps and explore the various applications to fully grasp the power of the slope-intercept form. By understanding this fundamental concept, you'll build a solid foundation for more advanced mathematical concepts and real-world problem-solving.
Latest Posts
Latest Posts
-
Two Thirds Of A Number Algebraic Expression
Apr 04, 2025
-
Is Photosynthesis A Chemical Or Physical Change
Apr 04, 2025
-
Convert 101 Degrees Fahrenheit To Celsius
Apr 04, 2025
-
How Many Minute In A Week
Apr 04, 2025
-
How Do Humans Impact Phosphorus Cycle
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about 3x 2y 16 In Slope Intercept Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
