3 Out Of 22 As A Percentage
listenit
May 24, 2025 · 5 min read
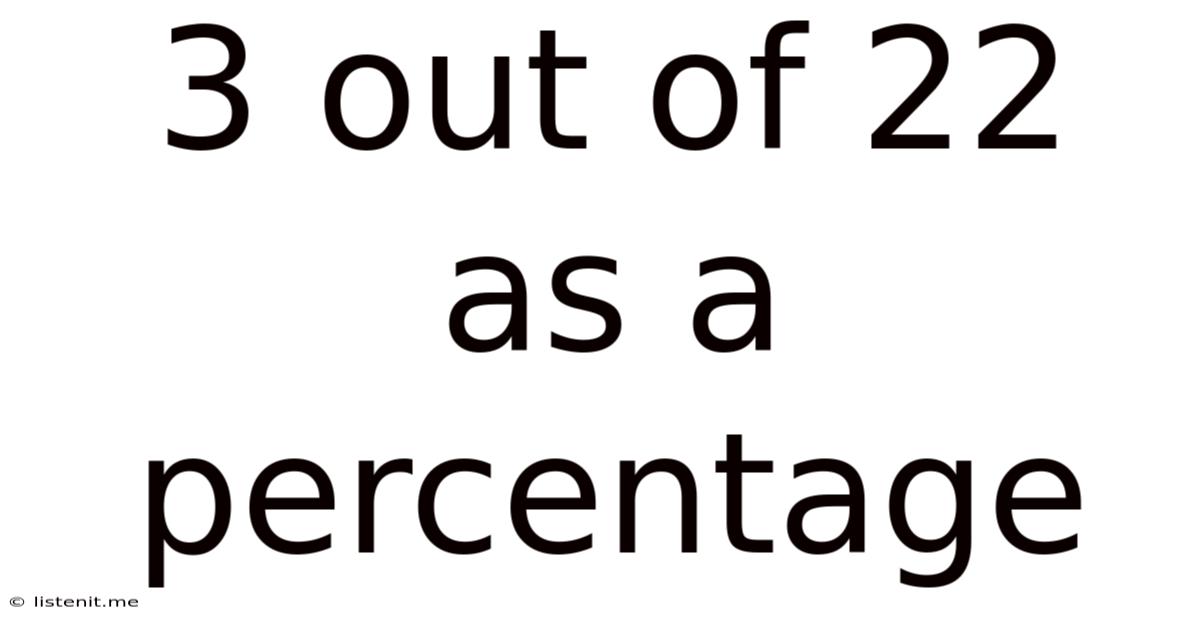
Table of Contents
3 Out of 22 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday finances to complex scientific analyses. Understanding how to convert fractions and ratios into percentages is crucial for interpreting data, making informed decisions, and effectively communicating numerical information. This comprehensive guide will delve into the specific calculation of "3 out of 22 as a percentage," exploring the methodology, providing practical examples, and expanding on the broader context of percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." When we say "x percent," we mean x out of every 100. For example, 50% means 50 out of 100, which is equivalent to one-half (1/2) or 0.5 as a decimal.
Percentages are versatile tools for comparing quantities, expressing proportions, and showcasing changes in values. They are frequently used in various fields including:
- Finance: Interest rates, discounts, tax calculations, profit margins.
- Science: Statistical analysis, experimental results, data representation.
- Business: Sales figures, market share, growth rates, performance indicators.
- Everyday Life: Tip calculations, recipe adjustments, understanding discounts in stores.
Calculating 3 Out of 22 as a Percentage
To calculate "3 out of 22" as a percentage, we follow these steps:
Step 1: Express the ratio as a fraction:
The phrase "3 out of 22" can be written as the fraction 3/22.
Step 2: Convert the fraction to a decimal:
Divide the numerator (3) by the denominator (22):
3 ÷ 22 ≈ 0.1363636...
Step 3: Convert the decimal to a percentage:
Multiply the decimal by 100 and add the "%" symbol:
0.1363636... × 100 ≈ 13.64%
Therefore, 3 out of 22 is approximately 13.64%. Note that we've rounded the result to two decimal places for practical purposes. The exact value is a recurring decimal.
Practical Applications and Examples
Understanding how to calculate percentages like "3 out of 22" has numerous practical applications. Here are a few examples:
Example 1: Test Scores:
Imagine a student answered 3 questions correctly out of a total of 22 questions on a test. Their percentage score would be approximately 13.64%. This allows for easy comparison of scores across different tests with varying numbers of questions.
Example 2: Sales Performance:
Suppose a salesperson made 3 successful sales out of 22 customer interactions. Their success rate would be about 13.64%. This metric helps track sales efficiency and identify areas for improvement.
Example 3: Survey Results:
If 3 out of 22 respondents in a survey selected a particular option, the percentage of respondents choosing that option would be roughly 13.64%. This helps in visualizing and interpreting survey data.
Example 4: Manufacturing Defects:
In a batch of 22 manufactured products, 3 were found to be defective. The defect rate is approximately 13.64%. This information is crucial for quality control and process improvement.
Different Methods for Calculating Percentages
While the method described above is straightforward, there are alternative approaches to calculating percentages, especially when dealing with more complex scenarios. These include:
- Using a calculator: Most calculators have a percentage function that simplifies the calculation. Simply enter 3 ÷ 22 and then multiply by 100.
- Using a spreadsheet program: Spreadsheet software like Microsoft Excel or Google Sheets offers built-in functions for percentage calculations. For example, in Excel, you could use the formula
= (3/22)*100to get the percentage. - Using proportions: You can set up a proportion: 3/22 = x/100. Solving for x gives you the percentage.
- Using mental math (for simpler cases): For simple fractions, you might be able to estimate the percentage mentally. For instance, knowing that 1/2 is 50%, you can approximate fractions based on their relationship to 1/2.
Beyond the Basics: Advanced Percentage Concepts
While understanding the basic calculation of "3 out of 22 as a percentage" is fundamental, mastering percentage calculations involves understanding more advanced concepts such as:
- Percentage change: This involves calculating the difference between two values as a percentage of the original value. This is frequently used to analyze growth or decline in various metrics. The formula is:
[(New Value - Old Value) / Old Value] x 100 - Percentage points: This refers to the absolute difference between two percentages. It's important to differentiate between a percentage change and a change in percentage points.
- Compound interest: This involves calculating interest on both the principal amount and accumulated interest. It's a crucial concept in finance and investments.
- Percentage yield: In investment contexts, this represents the return on investment expressed as a percentage of the original investment.
Troubleshooting Common Mistakes
When working with percentages, several common mistakes can lead to inaccurate results. Here are some points to keep in mind:
- Order of operations: Ensure you follow the correct order of operations (PEMDAS/BODMAS) when performing calculations involving multiple operations.
- Rounding errors: Rounding intermediate results can accumulate errors. It's generally better to round only the final answer.
- Units: Ensure that all values are expressed in consistent units before performing calculations.
- Misinterpreting percentage changes: Confusing percentage points with percentage change is a common error.
Conclusion
Calculating "3 out of 22 as a percentage" is a simple yet vital skill with far-reaching applications. Mastering this basic calculation forms a foundation for understanding more complex percentage-related concepts. By understanding the methodology, practicing with diverse examples, and being mindful of potential errors, you can confidently utilize percentages in various contexts to analyze data, make informed decisions, and effectively communicate numerical information. The ability to accurately and efficiently calculate and interpret percentages is an invaluable asset in numerous professional and personal settings. Remember to always double-check your work and use the method you find most comfortable and accurate.
Latest Posts
Latest Posts
-
8 2 9 As An Improper Fraction
May 24, 2025
-
What Is The Greatest Common Factor Of 7 And 21
May 24, 2025
-
Greatest Common Factor Of 24 And 96
May 24, 2025
-
12 More Than 8 2 Times A Number N
May 24, 2025
-
8 Out Of 10 In Percentage
May 24, 2025
Related Post
Thank you for visiting our website which covers about 3 Out Of 22 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.