12 More Than 8.2 Times A Number N
listenit
May 24, 2025 · 4 min read
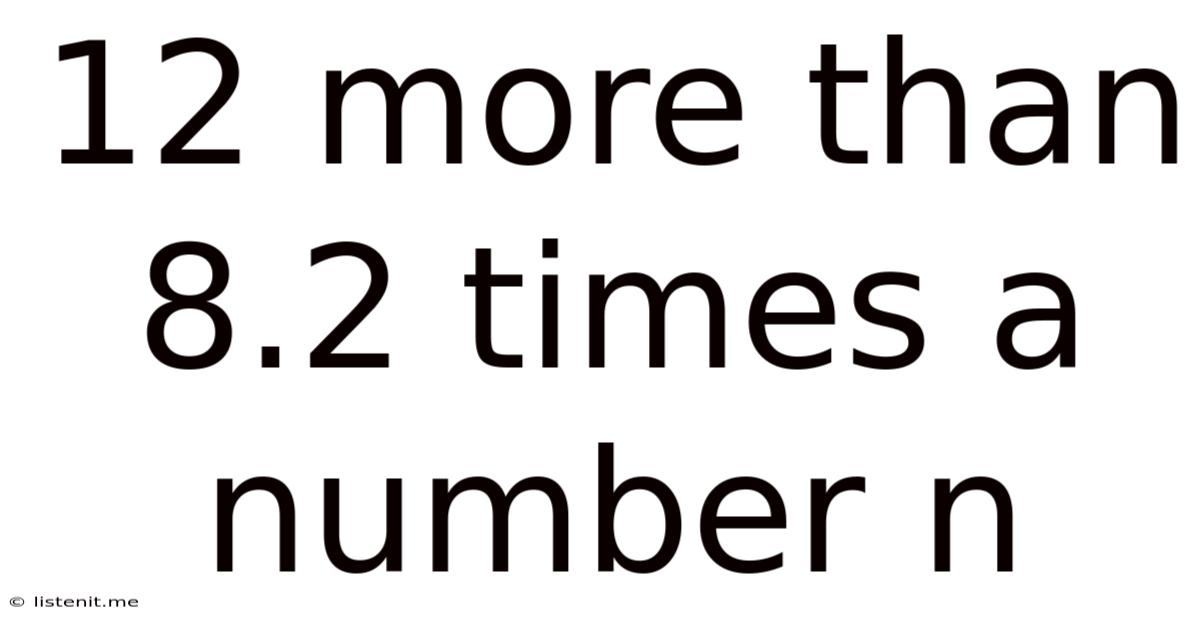
Table of Contents
12 More Than 8.2 Times a Number: A Deep Dive into Mathematical Expressions
This article explores the mathematical expression "12 more than 8.2 times a number n," dissecting its components, solving related equations, and extending the concept to various applications. We will delve into the intricacies of translating word problems into algebraic expressions, focusing on the crucial role of understanding keywords and their mathematical equivalents. Finally, we'll consider real-world scenarios where this type of expression finds practical use.
Understanding the Expression: Deconstructing the Problem
The phrase "12 more than 8.2 times a number n" represents a specific mathematical relationship. Let's break it down piece by piece:
-
"a number n": This represents an unknown value, typically denoted by the variable 'n'. It could be any real number.
-
"8.2 times a number n": This translates directly to the algebraic expression 8.2n. The word "times" signifies multiplication.
-
"12 more than": This indicates the addition of 12 to the previous expression. "More than" always implies addition.
Therefore, the complete algebraic representation of the phrase "12 more than 8.2 times a number n" is 8.2n + 12.
Solving Equations Involving the Expression
Now that we've translated the phrase into an algebraic expression, let's consider how to solve equations that incorporate it. The complexity of the solution depends on the context of the equation. Here are a few examples:
Example 1: Finding 'n' when the expression equals a given value
Let's say the expression 8.2n + 12 is equal to 34. To find the value of 'n', we set up and solve the following equation:
8.2n + 12 = 34
Steps to solve:
-
Subtract 12 from both sides: 8.2n = 22
-
Divide both sides by 8.2: n = 22 / 8.2 ≈ 2.68
Therefore, when the expression equals 34, the value of 'n' is approximately 2.68.
Example 2: Solving for 'n' with more complex equations
Consider a slightly more complex equation: 2(8.2n + 12) = 50
Steps to solve:
-
Distribute the 2: 16.4n + 24 = 50
-
Subtract 24 from both sides: 16.4n = 26
-
Divide both sides by 16.4: n = 26 / 16.4 ≈ 1.59
Example 3: Inequalities involving the expression
We can also explore inequalities. For example, let's find the values of 'n' for which 8.2n + 12 > 20.
Steps to solve:
-
Subtract 12 from both sides: 8.2n > 8
-
Divide both sides by 8.2: n > 8 / 8.2 ≈ 0.98
This means that the inequality is true for all values of 'n' greater than approximately 0.98.
Real-World Applications
The expression "12 more than 8.2 times a number n" might seem abstract, but it has several practical applications in various fields:
1. Financial Calculations
Imagine calculating the total cost of a product with a base price and additional charges. Let's say the base price of an item is 8.2 times the number of units (n) and there's a fixed shipping charge of $12. The total cost would be represented by 8.2n + 12.
This applies to many scenarios, from calculating the cost of materials in construction to determining the overall expense of a wholesale purchase.
2. Scientific Modeling
In science, this type of expression can be used to model various phenomena. For example, it could represent the growth of a population where 8.2n represents the natural growth rate and 12 represents a constant migration factor. This is a simplified model, of course, but illustrates the potential.
3. Business and Economics
In business, the expression could model profit calculations. Let's say 8.2n represents revenue generated per unit sold, and 12 represents fixed operating costs. The profit would be the difference between the revenue and the costs.
4. Engineering and Physics
In engineering and physics, this expression could model the relationship between different physical quantities. This might involve force, velocity, or other variables where a constant value (12) is added to a variable rate (8.2n).
Expanding the Concept: Variations and Extensions
The fundamental concept of "12 more than 8.2 times a number n" can be generalized. We can replace the numbers 12 and 8.2 with other constants and use different variables. This allows us to explore a broader range of mathematical relationships.
For example:
-
'a' more than 'b' times a number 'x': This generalizes the expression to bx + a, where 'a' and 'b' represent any constant and 'x' is the variable.
-
Exploring different operations: Instead of addition, we could explore subtraction, multiplication, or division.
Conclusion: Mastering Mathematical Expressions
Understanding how to translate word problems into algebraic expressions is a foundational skill in mathematics. The expression "12 more than 8.2 times a number n," although seemingly simple, provides a valuable framework for understanding the interplay between words and mathematical symbols. By mastering this concept, you build a strong foundation for tackling more complex mathematical problems across a wide array of disciplines. The ability to effectively solve equations and inequalities involving this and similar expressions is crucial for success in various academic and professional fields. Remember the importance of breaking down complex problems into smaller, manageable steps, and always double-check your work!
Latest Posts
Latest Posts
-
1 Of 15 Is What Percent
May 24, 2025
-
Greatest Common Factor Of 52 And 68
May 24, 2025
-
5 17 2 10 To The 3rd Power
May 24, 2025
-
What Is The Least Common Multiple Of 20 And 5
May 24, 2025
-
What Is The Prime Factorization Of 250
May 24, 2025
Related Post
Thank you for visiting our website which covers about 12 More Than 8.2 Times A Number N . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.