3 Is What Percent Of 11
listenit
May 24, 2025 · 4 min read
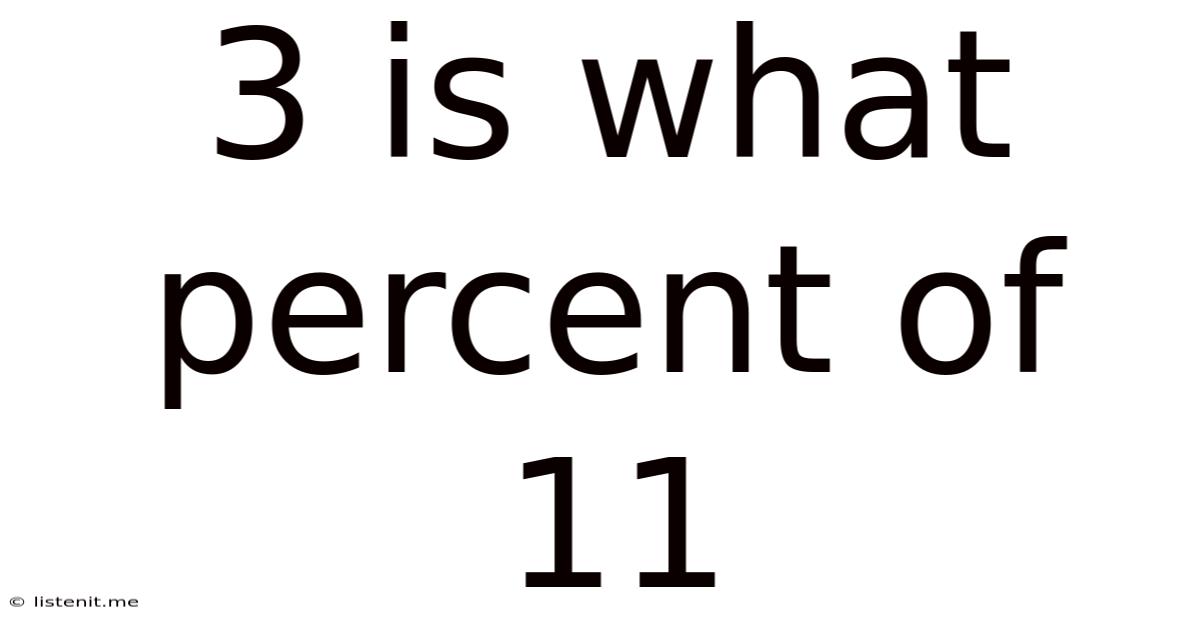
Table of Contents
3 is What Percent of 11? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with broad applications across various fields, from everyday budgeting and shopping to complex financial analyses and scientific research. Understanding how to determine what percentage one number represents of another is crucial for making informed decisions and interpreting data effectively. This comprehensive guide delves into the question, "3 is what percent of 11?", providing a step-by-step solution, exploring different approaches, and offering valuable insights into percentage calculations.
Understanding Percentages
Before we dive into the specifics of this problem, let's establish a firm grasp on the concept of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" signifies "per hundred," indicating the proportion of a whole. For example, 50% represents 50 parts out of 100, or one-half (50/100 = 1/2).
Percentages are used extensively because they offer a standardized way to compare different quantities and proportions. They provide a clear and concise representation of relative values, making them easy to interpret and understand.
Calculating "3 is What Percent of 11?" - Method 1: The Proportion Method
This method is arguably the most straightforward and intuitive way to solve this type of percentage problem. We'll set up a proportion:
- Part/Whole = Percentage/100
In this case:
- Part: 3
- Whole: 11
- Percentage: This is what we want to find (let's represent it with 'x')
Substituting the values into the proportion, we get:
3/11 = x/100
To solve for 'x', we cross-multiply:
3 * 100 = 11 * x
300 = 11x
Now, we divide both sides by 11:
x = 300/11
x ≈ 27.27
Therefore, 3 is approximately 27.27% of 11.
Calculating "3 is What Percent of 11?" - Method 2: The Decimal Method
This method involves converting the fraction to a decimal and then multiplying by 100 to express the result as a percentage.
First, we express the relationship as a fraction:
3/11
Next, we convert this fraction into a decimal by dividing 3 by 11:
3 ÷ 11 ≈ 0.2727
Finally, to convert this decimal to a percentage, we multiply by 100:
0.2727 * 100 ≈ 27.27%
Again, we arrive at the same answer: 3 is approximately 27.27% of 11.
Understanding the Significance of Approximation
Note that in both methods, we obtained an approximate answer (27.27%). This is because the fraction 3/11 is a non-terminating decimal; it continues infinitely. We rounded the decimal to two decimal places for practical purposes. The exact percentage is a recurring decimal. However, for most everyday applications, rounding to two decimal places provides sufficient accuracy.
Practical Applications of Percentage Calculations
The ability to calculate percentages accurately has widespread practical applications:
1. Financial Calculations:
- Interest Rates: Calculating simple and compound interest requires a thorough understanding of percentages.
- Discounts and Sales Tax: Determining the final price of an item after discounts and taxes involves percentage calculations.
- Investment Returns: Assessing the profitability of investments involves calculating percentage returns on investment.
- Budgeting: Allocating funds across different categories of a budget often requires working with percentages.
2. Statistical Analysis:
- Data Representation: Percentages are commonly used to represent proportions and distributions within datasets.
- Hypothesis Testing: Many statistical tests rely on percentage calculations to determine the significance of results.
- Surveys and Polls: Percentages are essential for summarizing and interpreting results from surveys and polls.
3. Everyday Life:
- Shopping: Comparing prices and determining the best deals often involves calculating discounts and sales taxes.
- Tipping: Calculating appropriate tips in restaurants and other service industries typically involves percentage calculations.
- Cooking and Baking: Many recipes use percentages to indicate the proportion of ingredients.
Beyond the Basics: Advanced Percentage Calculations
While the problem "3 is what percent of 11?" demonstrates a basic percentage calculation, the concept extends to more complex scenarios:
1. Percentage Increase and Decrease:
Calculating the percentage increase or decrease between two values is a common task. The formula for percentage change is:
[(New Value - Old Value) / Old Value] * 100%
2. Percentage Points:
It's crucial to differentiate between percentage points and percentages. A percentage point difference represents the absolute difference between two percentages, while a percentage change refers to the relative difference. For instance, an increase from 10% to 15% is a 5 percentage point increase, but a 50% increase in the percentage itself.
3. Compounding Percentages:
In situations involving repeated percentage changes, such as compound interest, the calculations become more involved. Understanding how compounding works is crucial for long-term financial planning.
4. Weighted Averages:
When dealing with multiple values carrying different weights, weighted averages need to be calculated, involving percentage weights.
Conclusion: Mastering Percentage Calculations
The ability to accurately calculate percentages is a versatile and indispensable skill. Whether it's for managing personal finances, analyzing data, or tackling more complex mathematical problems, a strong understanding of percentages empowers individuals to make informed decisions and interpret information effectively. By mastering the fundamental methods discussed in this guide—the proportion method and the decimal method—and exploring the advanced applications, one can confidently approach various percentage-related challenges. Remember that practice is key to solidifying this essential skill, so keep practicing different problems to hone your ability. The more you work with percentages, the more intuitive and effortless these calculations will become.
Latest Posts
Latest Posts
-
40 Of 35 Is What Number
May 24, 2025
-
How Old Is Someone From 1981
May 24, 2025
-
Greatest Common Factor Of 48 And 80
May 24, 2025
-
If Born In 1999 How Old Are You
May 24, 2025
-
How To Find 2 Sides Of A Right Triangle
May 24, 2025
Related Post
Thank you for visiting our website which covers about 3 Is What Percent Of 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.