3/4 Has How Many 1/8 In It
listenit
May 26, 2025 · 5 min read
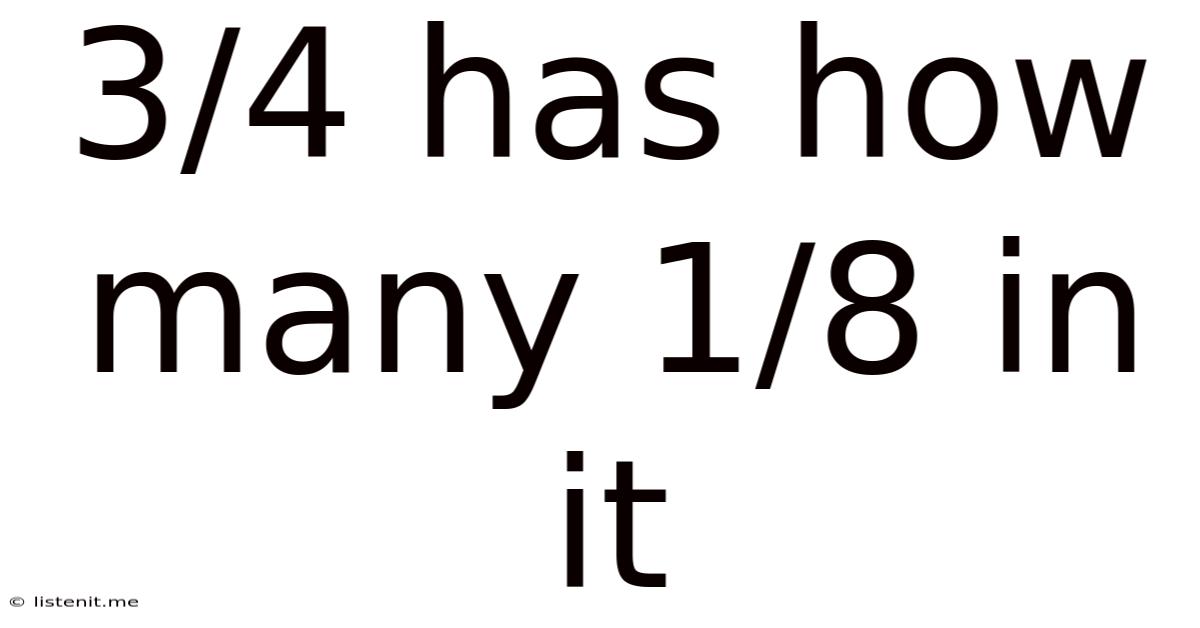
Table of Contents
3/4 Has How Many 1/8 in It? A Comprehensive Guide to Fraction Division
Understanding fractions is a cornerstone of mathematics, crucial for various applications from baking to engineering. A common question that arises, particularly in elementary and middle school mathematics, is: "How many 1/8 are there in 3/4?" This seemingly simple question opens the door to exploring fundamental concepts of fraction division and equivalent fractions. This comprehensive guide will not only answer this question but also equip you with the tools and understanding to tackle similar problems confidently.
Understanding Fractions: A Quick Refresher
Before diving into the problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) represents three parts, and the denominator (4) represents that the whole is divided into four equal parts.
Visualizing the Problem: The Power of Representation
One of the most effective ways to understand fraction division is through visualization. Imagine a pizza cut into eight equal slices (representing the denominator of 1/8). Now, consider that you have three-quarters of the pizza. How many 1/8 slices are there in 3/4 of the pizza?
This visual representation immediately suggests that we need to find the equivalent fraction of 3/4 that has a denominator of 8. This visual approach helps to build intuitive understanding and avoid confusion with the purely algorithmic approach.
Method 1: Finding Equivalent Fractions
This is perhaps the most straightforward method. The goal is to convert 3/4 into an equivalent fraction with a denominator of 8. To do this, we ask ourselves: "What number, when multiplied by the current denominator (4), will give us the desired denominator (8)?" The answer is 2 (4 x 2 = 8).
Since we multiplied the denominator by 2, we must also multiply the numerator by the same number to maintain the fraction's value. Therefore:
(3 x 2) / (4 x 2) = 6/8
Therefore, there are six 1/8's in 3/4.
This method emphasizes the concept of equivalent fractions – fractions that represent the same value despite having different numerators and denominators. Understanding equivalent fractions is crucial for various mathematical operations, including adding, subtracting, and comparing fractions.
Method 2: Fraction Division – The Formal Approach
While the equivalent fraction method is intuitive, the formal approach to solving this problem involves fraction division. The question "How many 1/8 are there in 3/4?" can be rewritten as a division problem:
3/4 ÷ 1/8
Dividing by a fraction is the same as multiplying by its reciprocal (inverting the numerator and denominator). The reciprocal of 1/8 is 8/1 (or simply 8). Therefore, the problem becomes:
3/4 x 8/1
Now, we multiply the numerators together and the denominators together:
(3 x 8) / (4 x 1) = 24/4
Simplifying the resulting fraction:
24/4 = 6
Again, we arrive at the answer: there are six 1/8's in 3/4. This method solidifies the understanding of fraction division as a crucial arithmetic operation.
Method 3: Using Decimal Equivalents (for Added Understanding)
While not strictly necessary, converting the fractions to decimals can provide an alternative perspective.
- 3/4 = 0.75
- 1/8 = 0.125
Now, we divide the decimal equivalent of 3/4 by the decimal equivalent of 1/8:
0.75 ÷ 0.125 = 6
This reinforces the previous results, showcasing that the same answer can be obtained through different methods. This approach offers a practical application of decimal conversions and their relevance in solving fractional problems.
Extending the Concept: Solving Similar Problems
The principles outlined above can be applied to a wide range of similar problems. For instance, let's consider how many 1/16 are in 3/4:
Method 1 (Equivalent Fractions):
First, find the equivalent fraction of 3/4 with a denominator of 16. Since 4 x 4 = 16, we multiply both the numerator and denominator by 4:
(3 x 4) / (4 x 4) = 12/16
Therefore, there are twelve 1/16's in 3/4.
Method 2 (Fraction Division):
3/4 ÷ 1/16 = 3/4 x 16/1 = 48/4 = 12
Again, the result is twelve. This exercise demonstrates the adaptability of these methods to various fractional contexts.
Real-World Applications: Where Fraction Division Matters
Understanding fraction division isn't just an academic exercise; it has practical applications in many real-world scenarios:
- Cooking and Baking: Recipes often require fractions of ingredients. Knowing how many 1/8 cups are in 3/4 cup is essential for accurate measurements.
- Construction and Engineering: Precise measurements are critical in construction and engineering. Calculations involving fractions are common in determining material quantities and dimensions.
- Finance: Understanding fractions is crucial for managing finances, calculating interest rates, and understanding portions of investments.
- Data Analysis: Data often involves fractions and percentages. Understanding these concepts is necessary for interpreting and analyzing data effectively.
Conclusion: Mastering Fractions for a Brighter Future
The seemingly simple question, "3/4 has how many 1/8 in it?" unveils a deeper understanding of fraction manipulation and division. By mastering these concepts, you equip yourself with essential skills applicable in various academic and real-world contexts. Whether you choose the equivalent fraction method, the formal division approach, or even the decimal conversion method, the key is to understand the underlying principles and to apply them confidently and accurately. Remember that visualization and practice are key to mastering these concepts and building a strong foundation in mathematics. Continue exploring different problems to solidify your understanding and build your confidence in tackling increasingly complex fractional equations.
Latest Posts
Latest Posts
-
Heat Pump Size Calculator By Square Footage
May 26, 2025
-
Write 2 49 100 As A Decimal Number
May 26, 2025
-
At 2am What Time Will It Be
May 26, 2025
-
Fill Dirt Calculator With Compaction Square Feet
May 26, 2025
-
1 Raised To The Power Of 5
May 26, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Has How Many 1/8 In It . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.