1 Raised To The Power Of 5
listenit
May 26, 2025 · 5 min read
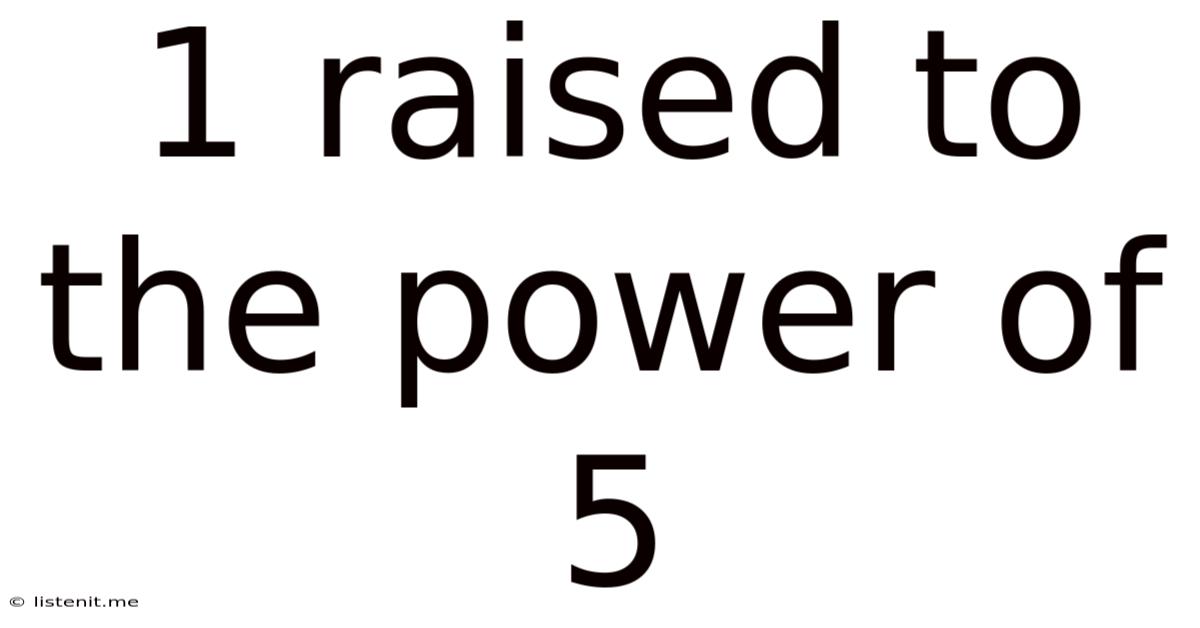
Table of Contents
1 Raised to the Power of 5: A Deep Dive into Exponents and Their Implications
The seemingly simple mathematical expression "1 raised to the power of 5," or 1⁵, might appear trivial at first glance. However, delving into this seemingly basic calculation opens a door to understanding fundamental concepts in mathematics, particularly exponents and their broader implications across various fields. This article will explore the calculation itself, the underlying principles of exponents, and the surprising ways this simple expression connects to more complex mathematical ideas.
Understanding Exponents
Before diving into 1⁵, let's establish a solid foundation in understanding exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the general form aⁿ, 'a' represents the base, and 'n' represents the exponent. Therefore, aⁿ means 'a' multiplied by itself 'n' times.
For example:
- 2³ = 2 × 2 × 2 = 8 (2 is the base, 3 is the exponent)
- 5² = 5 × 5 = 25 (5 is the base, 2 is the exponent)
- 10⁴ = 10 × 10 × 10 × 10 = 10,000 (10 is the base, 4 is the exponent)
Calculating 1 Raised to the Power of 5 (1⁵)
Now, let's address the core subject: 1⁵. Applying the definition of exponents, we simply multiply the base (1) by itself five times:
1⁵ = 1 × 1 × 1 × 1 × 1 = 1
The result, unsurprisingly, is 1. This outcome holds true regardless of the exponent; any positive integer power of 1 will always equal 1.
The Uniqueness of 1 as a Base
The number 1 possesses a unique property when used as a base in exponential expressions. This property stems directly from the multiplicative identity property in mathematics. The multiplicative identity property states that any number multiplied by 1 remains unchanged. Because of this, repeatedly multiplying 1 by itself results in 1, regardless of how many times the multiplication is performed.
This contrasts sharply with other bases. For instance, 2², 2³, 2⁴, etc., all yield different results. The same applies to any base other than 1. The constancy of the result when the base is 1 simplifies calculations and has significant implications in various mathematical contexts.
Extending the Concept: Negative and Zero Exponents
While we've focused on positive integer exponents, the concept of exponents extends to negative and zero exponents as well. Let's briefly explore how these apply to the base 1:
-
1⁰ = 1: Any number (except 0) raised to the power of 0 equals 1. This is a fundamental rule in mathematics.
-
1⁻ⁿ = 1: Any number raised to a negative exponent is the reciprocal of that number raised to the positive exponent. Therefore, 1⁻ⁿ = 1/1ⁿ = 1/1 = 1.
Applications of 1 Raised to the Power of n in Real-World Scenarios
Although 1⁵ seems insignificant, the broader concept of 1 raised to any power has practical applications in various fields:
-
Computer Science and Binary Systems: In binary systems (used extensively in computing), 1 represents the "on" state. Raising 1 to any power still results in 1, mirroring the persistent "on" state. This is fundamental to understanding boolean logic and digital circuitry.
-
Probability and Statistics: In probability calculations, the number 1 often represents certainty or an event that is guaranteed to occur. When dealing with probabilities, raising 1 to a power maintains the certainty of the event, regardless of the exponent.
-
Financial Modeling: In certain financial models, 1 can represent a base value or a constant factor. Raising 1 to various powers, within the model's framework, can simplify calculations and maintain the base value throughout the calculation.
-
Calculus and Limits: In the study of limits and calculus, dealing with expressions that involve 1 raised to a variable power often leads to simplifying calculations and reaching conclusions more easily.
-
Abstract Algebra: In abstract algebra, the multiplicative identity element (often denoted as 1) plays a crucial role in group theory and other areas. Its behavior under exponentiation is a key aspect of understanding these structures.
Comparing 1 to Other Bases
To fully appreciate the uniqueness of 1 as a base, let's compare it to other bases, focusing on the behavior of their respective powers:
| Base | Exponent 1 | Exponent 2 | Exponent 3 | Exponent 4 | Exponent 5 |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 4 | 8 | 16 | 32 |
| 3 | 3 | 9 | 27 | 81 | 243 |
| 10 | 10 | 100 | 1000 | 10000 | 100000 |
This table clearly demonstrates that while other bases produce exponentially increasing results, the base 1 remains constant regardless of the exponent.
The Significance of the Constant Result
The constant result of 1, when raised to any power, has implications for simplification and predictability in mathematical expressions and models. It allows for a degree of certainty and predictability that is not present with other bases. This stability is invaluable in many fields where mathematical accuracy and predictability are paramount.
Mathematical Properties and Identities Related to 1
Several mathematical identities and properties are directly related to the number 1, emphasizing its unique role in mathematical operations:
-
Multiplicative Identity: As previously mentioned, 1 is the multiplicative identity. Any number multiplied by 1 equals itself.
-
Division by 1: Dividing any number by 1 yields the same number.
-
Powers of 1: As extensively discussed, 1 raised to any power (positive, negative, or zero) equals 1.
-
Roots of 1: The nth root of 1 is always 1 (for positive integers n).
Conclusion: The Unassuming Power of 1
While 1⁵ might seem like a trivial calculation, its exploration unveils the fascinating world of exponents and the unique properties of the number 1. Its consistent output, regardless of the exponent, simplifies calculations and plays a crucial, albeit often understated, role in various mathematical fields and real-world applications. From computer science to finance, the seemingly simple principle of 1 raised to any power underlies complex systems and calculations, highlighting the profound importance of even the most basic mathematical concepts. Understanding the behavior of 1 as a base in exponential expressions provides a crucial foundation for more advanced mathematical studies and a deeper appreciation of the elegance and consistency within mathematics.
Latest Posts
Latest Posts
-
Who Created The First Psychology Lab
May 27, 2025
-
What Does It Mean That Neurons Are Excitable
May 27, 2025
-
Viscoelastic Materials That Lubricate Under Load
May 27, 2025
-
How Much Does Ferritin Drop After Period
May 27, 2025
-
What Does P A I Stand For
May 27, 2025
Related Post
Thank you for visiting our website which covers about 1 Raised To The Power Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.