3 4 Divided By 7 8
listenit
Apr 03, 2025 · 5 min read
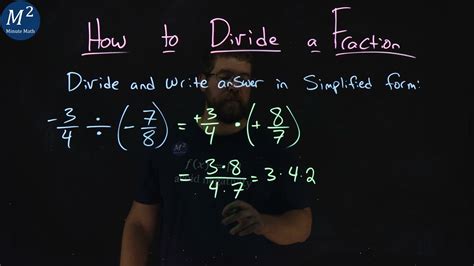
Table of Contents
3/4 Divided by 7/8: A Comprehensive Guide to Fraction Division
Dividing fractions can seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through dividing 3/4 by 7/8, explaining the underlying principles and offering practical examples to solidify your understanding. We'll explore different methods, address common pitfalls, and provide you with the tools to tackle similar fraction division problems with confidence.
Understanding Fraction Division
Before diving into the specific problem of 3/4 divided by 7/8, let's establish a firm grasp of the fundamentals of fraction division. The core concept is to invert (reciprocate) the second fraction and then multiply. This seemingly simple step is derived from the mathematical properties of fractions and division.
The Reciprocal: The Key to Fraction Division
The reciprocal, or multiplicative inverse, of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2. The product of a fraction and its reciprocal always equals 1. This property is crucial in simplifying the division of fractions.
Why We Invert and Multiply
When we divide by a fraction, we're essentially asking "how many times does the second fraction fit into the first fraction?" Inverting and multiplying provides a mathematically elegant way to answer this question. It transforms the division problem into a multiplication problem, which is generally easier to manage.
Solving 3/4 Divided by 7/8 Step-by-Step
Now, let's tackle our specific problem: 3/4 ÷ 7/8. We'll break it down step-by-step to ensure complete clarity.
Step 1: Identify the dividend and the divisor.
In our problem, 3/4 is the dividend (the number being divided), and 7/8 is the divisor (the number we're dividing by).
Step 2: Invert (reciprocate) the divisor.
The reciprocal of 7/8 is 8/7.
Step 3: Change the division sign to a multiplication sign.
Our problem now becomes: 3/4 × 8/7.
Step 4: Multiply the numerators and the denominators.
- Multiply the numerators: 3 × 8 = 24
- Multiply the denominators: 4 × 7 = 28
This gives us the fraction 24/28.
Step 5: Simplify the fraction (if possible).
Both 24 and 28 are divisible by 4. Simplifying the fraction, we get:
24/28 = 6/7
Therefore, 3/4 divided by 7/8 equals 6/7.
Alternative Methods: Visualizing Fraction Division
While the invert-and-multiply method is efficient, visualizing the division can aid understanding, especially for beginners. Let's explore a visual approach.
Imagine you have a rectangular pizza cut into four equal slices. You possess three of these slices (3/4 of the pizza). You want to share these three slices equally among groups, where each group receives 7/8 of a pizza. How many groups can you serve?
This visual representation emphasizes the concept of "how many times does 7/8 fit into 3/4?" While this visual approach doesn't directly lead to a calculation, it provides an intuitive understanding of the division process. The mathematical solution (6/7) indicates that you can serve a little less than one full group.
Practical Applications: Real-World Scenarios
Fraction division is encountered frequently in various real-world situations:
- Cooking and Baking: Adjusting recipes, scaling ingredients up or down.
- Sewing and Crafting: Calculating fabric needs, determining material quantities.
- Construction and Engineering: Measuring materials, calculating proportions in blueprints.
- Finance and Budgeting: Dividing resources, calculating percentages of income.
- Data Analysis: Working with proportions and ratios in datasets.
Mastering fraction division is therefore a valuable skill applicable across numerous fields.
Common Mistakes to Avoid
Several common mistakes can occur when dividing fractions:
- Forgetting to invert: The most prevalent error is neglecting to invert the divisor before multiplying. Remember, inversion is crucial for accurate results.
- Incorrect multiplication: Errors in multiplying the numerators and denominators can lead to inaccurate answers. Double-check your multiplication to ensure accuracy.
- Failure to simplify: Leaving the answer as an unsimplified fraction can obscure the true value. Always simplify the fraction to its lowest terms.
- Confusing division with subtraction or addition: Fraction division is distinct from other arithmetic operations. Understanding the concept of reciprocation is essential.
Expanding Your Knowledge: Further Exploration
Understanding the principles of fraction division empowers you to tackle more complex problems. Consider exploring:
- Dividing mixed numbers: Learn how to convert mixed numbers into improper fractions before applying the division method.
- Dividing fractions with decimals: Practice converting decimals to fractions or vice versa before performing the division.
- Dividing complex fractions: Master the art of simplifying complex fractions before applying the division method.
- Using calculators for fraction division: Familiarity with calculator functions for fraction division can enhance efficiency.
Conclusion: Mastering Fraction Division
Dividing fractions might appear challenging initially, but with consistent practice and a clear understanding of the process, it becomes a manageable skill. Remember the key steps: invert the divisor, change the division sign to multiplication, multiply the numerators and denominators, and simplify the resulting fraction. By mastering this skill, you equip yourself with a valuable tool for problem-solving in various real-world scenarios. Through consistent practice and a focus on understanding the underlying principles, you can confidently tackle any fraction division problem. Don't hesitate to revisit the steps, practice with different problems, and use visual aids to solidify your understanding. Remember, the key is to practice regularly and gradually increase the complexity of the problems you attempt. With persistence, you’ll master this essential mathematical skill.
Latest Posts
Latest Posts
-
1 Pint Is How Many Lbs
Apr 03, 2025
-
Does Dry Ice Evaporate Or Melt
Apr 03, 2025
-
Is Salt A Heterogeneous Or Homogeneous
Apr 03, 2025
-
What Is 3 And 1 2 As A Decimal
Apr 03, 2025
-
Which Subatomic Particle Contributes To The Mass Of An Atom
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Divided By 7 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
