3/4 + 3/4 Equals How Many Cups
listenit
Apr 02, 2025 · 5 min read
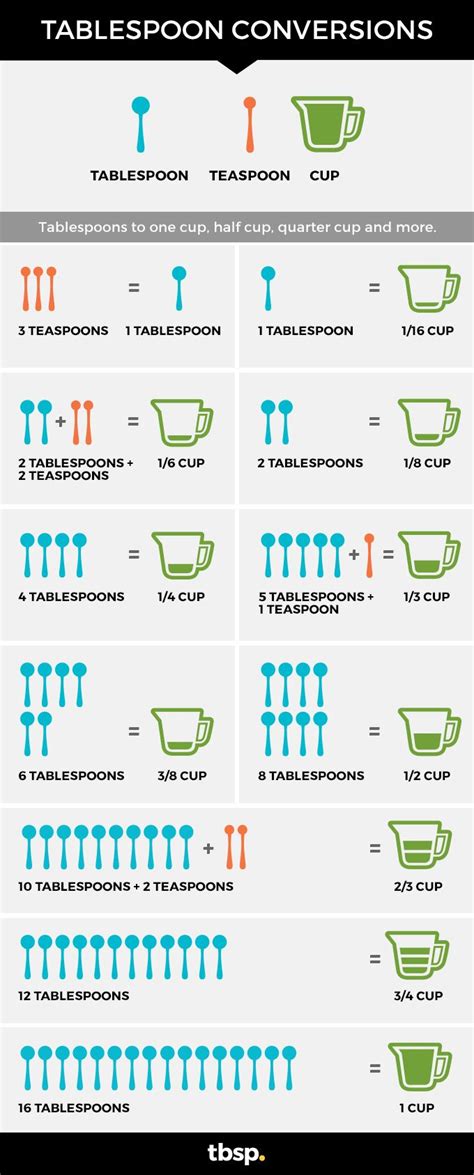
Table of Contents
3/4 + 3/4 Equals How Many Cups: A Comprehensive Guide to Fraction Addition in Baking
Adding fractions might seem daunting, especially when dealing with culinary measurements. But understanding this fundamental concept is crucial for baking success. This comprehensive guide will not only answer the question "3/4 + 3/4 equals how many cups?" but also delve into the underlying principles of fraction addition, providing you with the knowledge and confidence to tackle any fractional measurement in your baking endeavors.
Understanding Fractions in Baking
Fractions are an essential part of baking recipes. They represent parts of a whole, in this context, a whole cup. A recipe might call for ¾ cup of flour, ½ cup of sugar, or ⅛ cup of baking powder. Accurately measuring these fractions is key to achieving the desired outcome. Improper measurements can result in a cake that’s too dense, a pie crust that's too crumbly, or cookies that spread too thin.
What is 3/4 of a Cup?
Before we add fractions, let's understand what 3/4 of a cup represents. The number on the bottom (4) is the denominator, indicating the number of equal parts the whole cup is divided into. The number on top (3) is the numerator, showing how many of those equal parts we're using. Therefore, 3/4 cup means we're using 3 out of 4 equal parts of a cup.
Visualizing Fractions
Imagine a standard measuring cup divided into four equal sections. 3/4 of a cup would represent three of those four sections filled. This visual representation helps to solidify the understanding of fractional measurements.
Adding Fractions: A Step-by-Step Guide
Now, let's tackle the main question: 3/4 + 3/4. Adding fractions with the same denominator (the bottom number) is relatively straightforward.
Step 1: Check the Denominators
In our equation, both fractions have a denominator of 4. This is crucial because it means we're dealing with the same sized parts of a whole.
Step 2: Add the Numerators
The next step involves adding the numerators (the top numbers) while keeping the denominator unchanged. Therefore, 3 + 3 = 6.
Step 3: Write the Result
This gives us the fraction 6/4. This represents six parts of a cup when the cup is divided into four equal parts.
Step 4: Simplify (If Necessary)
The fraction 6/4 is an improper fraction because the numerator is larger than the denominator. We can simplify this by dividing the numerator by the denominator: 6 ÷ 4 = 1 with a remainder of 2. This can be expressed as 1 and 2/4.
Step 5: Further Simplification
The fraction 2/4 can be further simplified by dividing both the numerator and denominator by their greatest common divisor (2): 2 ÷ 2 = 1 and 4 ÷ 2 = 2. This simplifies to 1/2.
Step 6: Final Answer
Therefore, the final answer to 3/4 + 3/4 is 1 ½ cups.
Practical Applications in Baking
Understanding fraction addition is essential for accurate baking. Let’s explore some practical scenarios:
Example 1: Doubling a Recipe
Suppose a recipe calls for ¾ cup of butter. If you want to double the recipe, you need to add ¾ cup + ¾ cup, which, as we've established, equals 1 ½ cups of butter.
Example 2: Combining Ingredients
Imagine a recipe requiring ¾ cup of flour and ¾ cup of sugar. To determine the total amount of dry ingredients, you would add ¾ + ¾ = 1 ½ cups. This helps in preparing the correct amount of mixing bowls or understanding how much space these ingredients will occupy.
Example 3: Adjusting Recipe Yields
Let’s say a recipe yields 12 cookies using ¾ cup of chocolate chips. If you want to make twice the number of cookies (24), you’ll need to double the amount of chocolate chips, resulting in 1 ½ cups.
Beyond 3/4 + 3/4: Adding Other Fractions
The principles of adding fractions with the same denominator can be extended to other baking scenarios. Here’s how you would approach adding fractions with a common denominator:
Example: 1/8 + 3/8 + 5/8
- Add the numerators: 1 + 3 + 5 = 9
- Keep the denominator: The denominator remains 8.
- Result: 9/8
- Simplify: 9/8 is an improper fraction. 9 ÷ 8 = 1 with a remainder of 1. This simplifies to 1 ⅛.
Adding Fractions with Different Denominators
Adding fractions with different denominators requires a bit more work. This involves finding the least common denominator (LCD) – the smallest number that both denominators can divide into evenly.
Example: 1/2 + 1/4
- Find the LCD: The LCD of 2 and 4 is 4.
- Convert to Equivalent Fractions: Convert 1/2 to an equivalent fraction with a denominator of 4 by multiplying both the numerator and denominator by 2: (1 x 2) / (2 x 2) = 2/4
- Add the Fractions: 2/4 + 1/4 = 3/4
- Simplify: In this case, 3/4 is already in its simplest form.
Mastering Fractions: Tips and Tricks for Bakers
- Use a Measuring Cup with Markings: Invest in a measuring cup with clear markings for various fractions. This will help visualize and accurately measure ingredients.
- Practice Makes Perfect: The more you practice adding fractions, the more comfortable and confident you will become. Start with simple additions and gradually move on to more complex ones.
- Online Resources: Several online calculators and tutorials can assist you in adding fractions and converting between improper and mixed fractions.
- Convert to Decimals: You can convert fractions to decimals for easier addition. For example, 3/4 = 0.75. Adding 0.75 + 0.75 = 1.5, which is equivalent to 1 ½.
Conclusion: Baking Success Through Fractional Mastery
Understanding fraction addition is a fundamental skill for every baker. Mastering this concept allows for precise measurements, leading to consistent and delicious baking results. While the simple equation 3/4 + 3/4 = 1 ½ cups might seem trivial, it unlocks a deeper understanding of how fractions work, enabling you to confidently tackle more complex baking recipes. So, grab your measuring cups and start baking – your culinary creations will thank you!
Latest Posts
Latest Posts
-
What Is 5 6 As A Decimal
Apr 03, 2025
-
The Conjugate Base Of Hso4 Is
Apr 03, 2025
-
Examples Of Gay Lussacs Law In Real Life
Apr 03, 2025
-
Law Of Sines And Law Of Cosines Word Problems
Apr 03, 2025
-
18 Is What Percent Of 36
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about 3/4 + 3/4 Equals How Many Cups . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
